Question

В прямоугольном треугольнике проведена биссектриса угла,
равного 60°. Найдите длину этой биссектрисы, если она короче
большего катета на 2 см.
помогите пожалуйста отдам 60 баллов

Answer 1

Ответ:   биссектриса  ВК=4 см .

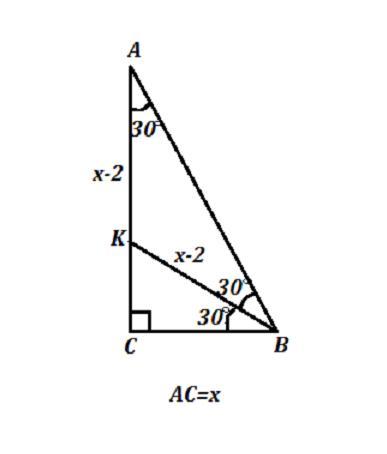
ΔАВС ,  ∠С=90° ,  ∠В=60°  ,  ВК - биссектриса  ⇒   ∠СВК=∠АВК=30°  .

ВК короче АС на 2 см .  Найти ВК .

Если в прямоугольном треугольнике один острый угол равен 60° , тогда второй острый угол равен  ∠А=90°-60°=30°  .

Против большего угла лежит большая сторона. Значит катет АС, лежащий против угла в 60° , больше катета ВС, лежащего против угла в 30° .

Так как в ΔАВК два угла равны по 30° , ∠А=∠АВК=30° , то этот треугольник равнобедренный и  АК=ВК .

Обозначим АС=х , тогда по условию  ВК=х-2 (см) , и  АК=х-2  (см) .

Рассм. ΔВКС , ∠С=90° , ∠СВК=30° . Против угла в 30° лежит катет, равный половине гипотенузы  то есть  $CK=\dfrac{x-2}{2}=\dfrac{x}{2}-1$  .

$AC=CK+AK\ \ \Rightarrow \ \ \ x=(\dfrac{x}{2}-1)+(x-2)\ \ ,\ \ \dfrac{x}{2}=1+2\ \ ,\\\\\dfrac{x}{2}=3\ \ ,\ \ x=6$

Тогда   $BK=x-2=6-2=4$  (cм) .