Предмет: Математика,
автор: maksik30082006
20 баллов срочно пожалуйста
Приложения:
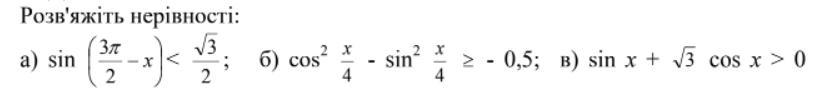
Ответы
Автор ответа:
0
Ответ:
a)
б)
в)
Пошаговое объяснение:
а) Решить неравенство
Применим формулы приведения и получим :
б) Решить неравенство
Применим формулу косинуса двойного угла
и получим
Пусть
Тогда
в) Решить неравенство
Воспользуемся методом введения вспомогательного угла
Пусть
#SPJ1
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: vilka0990
Предмет: Русский язык,
автор: влад1483
Предмет: Математика,
автор: sapyhina99
Предмет: Математика,
автор: irina19723