Предмет: Математика,
автор: onikamila9
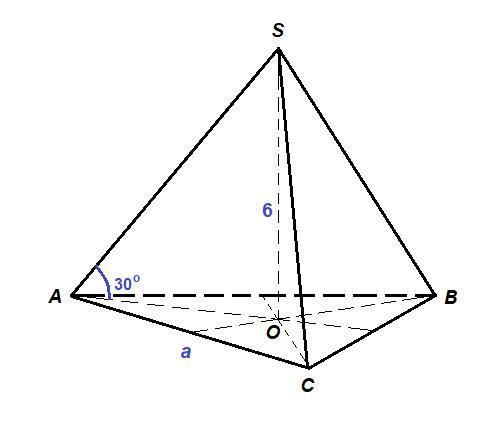
У правильній трикутній піраміді бічне ребро з площиною основи утворює кут 30°. Висота піраміди - 6 см.
Обчисли сторону основи піраміди.
Ответы
Автор ответа:
1
Ответ:
Сторона основания равна 18 см.
Пошаговое объяснение:
Так как пирамида правильная, то основание - правильный треугольник и высота пирамиды проецируется в центр основания.
SO - высота пирамиды, SO = 6 см, О - центр правильного треугольника АВС.
АО - проекция бокового ребра SA на плоскость основания, значит
∠SAO = 30° - угол наклона бокового ребра к плоскости основания.
ΔSAO: ∠SOA = 90°,
см
АО - радиус описанной около треугольника АВС окружности.
а = 18 см
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: катрин196
Предмет: Другие предметы,
автор: Djdhc
Предмет: Русский язык,
автор: Altai04a
Предмет: Английский язык,
автор: galcenkovtimofe
Предмет: Биология,
автор: annachanskp06yi3