Question

B$_{1}$ и C$_{1}$ середины AB и AC

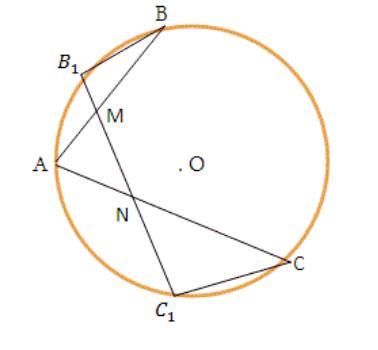
доказать что AM = AN

Answer 1

Ответ:

Так как $B_{1}$ и $C_{1}$середины АВ и АС ⇔

$AB_{1}$ =$B_{1}B$ = $\frac{1}{2}$ АВ

$C_{1}A$= $C_{1}C$= $\frac{1}{2}$СA

$NCC_{1}, NC_{1}C, MB_{1}B, MBB_{1}$  вписанные углы опираются на следующие дуги

$C_{1}A B_{1}C BC_{1} AB_{1}$

⇔

∠$NCC_{1}$=$\frac{CA}{4}$

∠NC$_{1}$C=$\frac{B_{1}C}{2} = \frac{360-CB_{1}}{2} = \frac{360-CA-AB_{1}}{2} = \frac{360-CA-AB/2}{2} = 180 -\frac{CA}{2} -\frac{AB}{4}$

∠$MB_{1}B$= $\frac{BC_{1}}{2} = \frac{BC+CC_{1}}{2} = \frac{360 - CB +CA/2}{2} = 180 - \frac{CB}{2} + \frac{CA}{4} = 180 - \frac{CA}{2} - \frac{AB}{2} + \frac{CA}{4} = 180 - \frac{CA}{4} - \frac{AB}{2}$

∠MB$B_{1}$ = $\frac{AB_{1}}{2} = \frac{AB}{4}$

Так как  сумма внутренних углов всех треугольников равна 180° ⇒

из Δ$MBB_{1}$

∠$NCC_{1} + NC_{1}C+ CNC_{1} = 180$°

получается

∠$CNC_{1}$= ∠$BMB_{1}$ = $\frac{AB+AC}{4}$

как противоположные углы  ∠$CNC_{1} = ANM, BMB_{1} = AMN$

значит если ∠$CNC_{1}$= ∠$BMB_{1}$= $\frac{AB+AC}{4}$  

тогда  ∠ANM = ∠AMN

⇔

ΔAMN  равноб.

⇔ AM= AN