Предмет: Математика,
автор: 21l04x
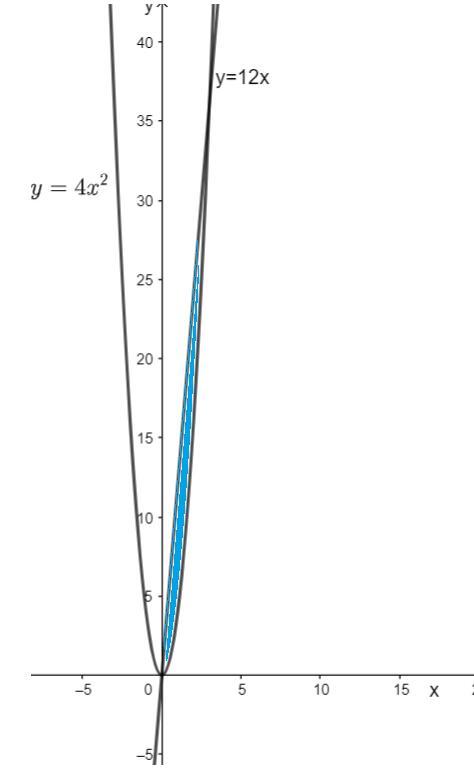
вычислите площадь фигуры, ограниченной линиям y=4x2 и y=12x
Ответы
Автор ответа:
1
Ответ:
Площадь фигуры равна 18 кв. ед.
Пошаговое объяснение:
Вычислить площадь фигуры, ограниченной линиями
Выполним рисунок.
Графиком функции является парабола, ветви которой направлены вверх с вершиной в точке (0; 0) .
Графиком функции является прямая, которая проходит через точки (0;0) и (1; 12)
Найдем абсциссы точек пересечения графиков, решив уравнение
Полученная фигур не является криволинейной трапецией, поэтому ее площадь
Значит, площадь фигуры равна 18 кв. ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ellvina5kashka
Предмет: Русский язык,
автор: peri011
Предмет: Русский язык,
автор: irkdfffff
Предмет: Английский язык,
автор: MayaAllahverdueva
Предмет: Геометрия,
автор: pavel3326