Предмет: Алгебра,
автор: mhislox
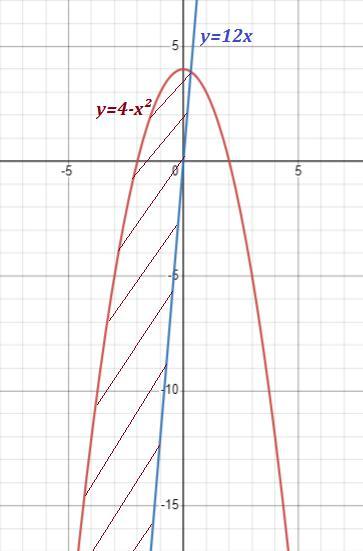
вычислите площадь фигуры ограниченной линиями у=4-х^2 и у=12х
Ответы
Автор ответа:
0
Ответ:
Точки пересечения.
- парабола с ветвями, направленными вниз .
- прямая, проходящая через начало координат .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: тимур30000
Предмет: Английский язык,
автор: Princess115
Предмет: Другие предметы,
автор: максоечик
Предмет: Математика,
автор: natalyakozlova4