помогите пожалуйста, фото закрепила.
Ответы
Ответ:
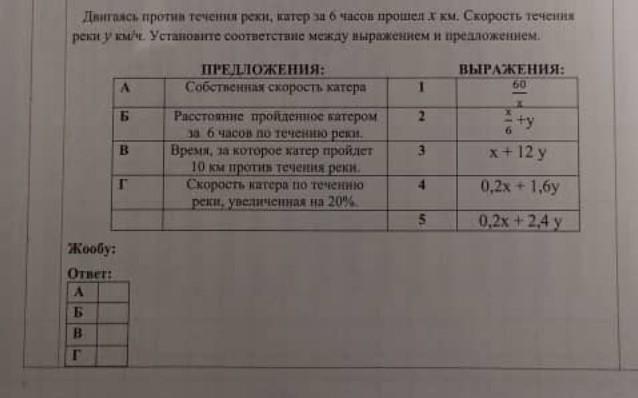
А собственная скорость катера ответ 2;
Б расстояние, пройденное катером за 6 часов по течению реки ответ 3 ;
В время, за которое пройдет катер 10 км против течения реки ответ 1;
Г скорость катера по течению реки, увеличенная на 20% ответ 5 .
Пошаговое объяснение:
Двигаясь против течения реки, катер за 6 часов прошел х км.
Для того чтобы найти скорость, надо расстояние разделить на время.
Поэтому км/ч - это скорость катера против течения реки.
По условию задана скорость течения реки y км/ч
Тогда собственная скорость катера будет равна: надо к скорости катера против течения прибавить скорость течения
км/ч
Значит,
А собственная скорость катера ответ 2
Надо найти расстояние, пройденное катером за 6 часов по течению реки. Для этого найдем скорость катера по течению реки: к собственной скорости надо прибавить скорость течения
(км/ч) - скорость катера по течению реки.
Найдем расстояние, которое пройдет катер за 6 часов при полученной скорости.
Чтобы найти расстояние надо скорость умножить на время
Тогда
(км) - расстояние, пройденное катером за 6 часов по течению реки
Значит,
Б расстояние, пройденное катером за 6 часов по течению реки ответ 3
Время, за которое пройдет катер 10 км против течения реки.
Чтобы найти время, надо расстояние разделить на скорость.
(ч) - время, необходимое катеру на 10 км против течения реки.
В время, за которое пройдет катер 10 км против течения реки ответ 1
Надо найти скорость катера по течению реки, увеличенную на 20%
(км/ч) - скорость катера по течению реки.
Увеличим ее на 20 %, то есть она будет составлять 120% . Представим % в виде дроби и найдем дробь от числа
120%= 1,2
(км/ч) - увеличенная на 20% скорость катера по течению реки.
Г скорость катера по течению реки, увеличенная на 20% ответ 5
#SPJ1