Question

Даю 100 баллов, помогите пожалуйста, СРОЧНО!
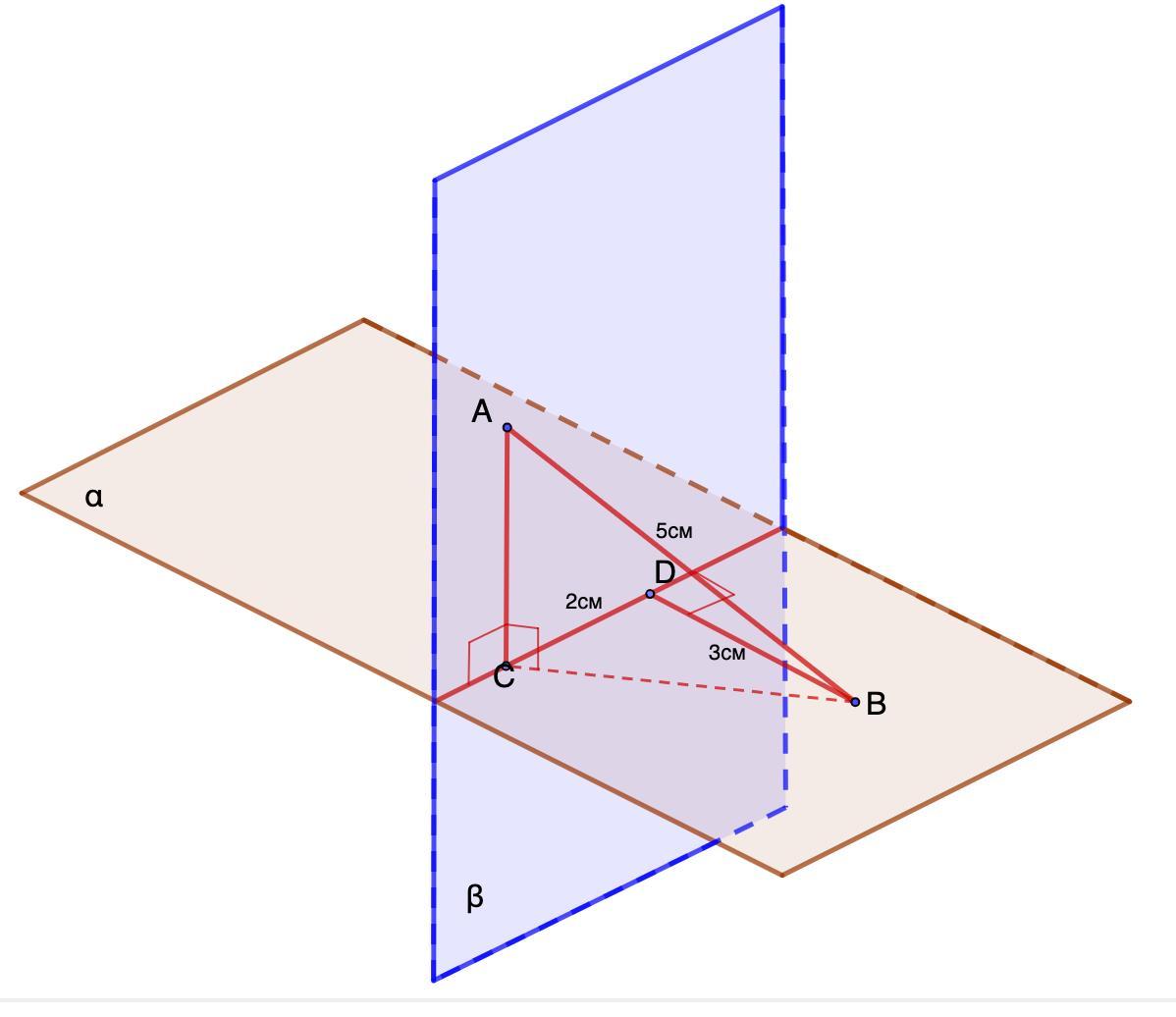
Из точек A и B, принадлежащих двум перпендикулярным плоскостям, проведены в них перпендикуляры AC и BD к линии пересечения плоскостей. Найти отрезок AC, если AB = 5 см, BD = 3 см, CD = 2 см.
Пожалуйста, распишите подробно, с рисунком. Заранее спасибо

Answer 1

Ответ:

Отрезок АС равен 2√3 см.

Пошаговое объяснение:

Из точек A и B, принадлежащих двум перпендикулярным плоскостям, проведены в них перпендикуляры AC и BD к линии пересечения плоскостей. Найти отрезок AC, если AB = 5 см, BD = 3 см, CD = 2 см.

Дано: α ⊥ β;

α ∩ β = CD;

AC ⊥ CD; BD ⊥ CD.

AB = 5 см, BD = 3 см, CD = 2 см.

Найти: АС.

Решение:

1. Рассмотрим ΔСDB - прямоугольный.

BD = 3 см, CD = 2 см.

По теореме Пифагора найдем СВ:

СВ² = CD² + DB² = 4 + 9 = 13

CB = √13 (см)

2. Рассмотрим ΔАВС.

АС ⊥ СD (условие)

• Если две плоскости взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.

⇒ АС ⊥ α

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости, проходящей через точку пересечения.

⇒ АС ⊥ СВ.

⇒ ΔАВС - прямоугольный.

По теореме Пифагора найдем АС:

АС² = АВ² - СВ² = 25 - 13 = 12

АС = √12 = 2√3 (см)

Отрезок АС равен 2√3 см.

#SPJ1