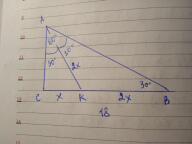
В прямоугольном треугольнике катет длиною 18 см прилегает к углу 30°. Найти длину биссектрисы другого острого угла треугольника. Только решение для 7 класса
Ответы
∆ АВС, <С=90° , <В=30° , АК биссектриса. По теореме о сумме углов треугольника, второй острый угол <А=60° . И именно его биссектриса делит пополам, <САК=<КАВ=30° . Пусть в ∆АКС , сторона СК=х, тогда АК=2х по свойству угла в 30° . В ∆ АКВ, два угла <В=<КАВ=30° =>АК=КВ. Тогда катет СВ=СК+КВ и СК=18=> х+2х=18, х=6 => АК=2*6=12(см).
Ответ:
12 см.
Объяснение:
Дано: ΔАВС, ∠С=90°, АК - биссектриса, ∠В=30°, ВС=18 см. АК - ?
∠ВАС=90-30=60° по свойству острых углов прямоугольного треугольника; ∠КАС=∠КАВ=60:2=30° по определению биссектрисы.
ΔСАК; пусть СК=х см, тогда АК=2х см по свойству катета, лежащего против угла 30°
ΔАВК - равнобедренный, т.к. углы при его основании равны, значит ВК=АК=2х см.
ВС=х+2х=18 см; 3х=18 см, х=6 см.
СК=6 см, АК=6*2=12 см.