Question

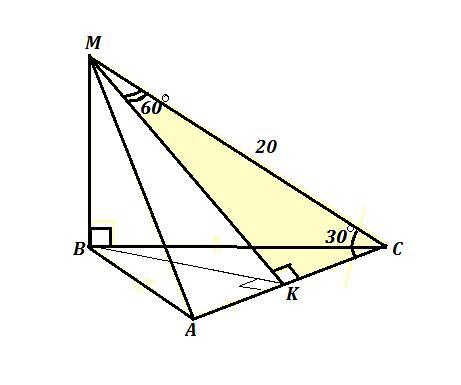
Из вершины В равнобедренного треугольника АВС (АВ=ВС) к его плоскости проведен перпендикуляр ВМ. Точка К – середина стороны АС. Чему равна длина отрезка МК, если МС = 20 см; а угол СМК равен 60°?
А) 10 см;
Б) 10 см;
В) 20 см;
Г) определить невозможно

Answer 1

Решение.

ΔАВС равнобедренный, АВ=ВС ,  ВМ ⊥ АВС ,  АК=КС   ⇒  точка К - середина стороны АС  и ВК - медиана, которая одновременно является высотой в равнобедренном треугольнике , значит ВК ⊥ АС ,  ∠ВКС=90° .  МС=20 см .

Проведена МК . В треугольнике АМС она является медианой , так как по условию АК=КС .

МК также является высотой в ΔАМС, так как по теореме о трёх перпендикулярах  МК - наклонная, ВК - её проекция на плоскость АВС, причём ВК ⊥ АС, значит и наклонная МК будет перпендикуляр-

на АС ,  МК ⊥ АС  ⇒  ΔМКС - прямоугольный, по условию

∠СМК=60° , значит  ∠ВСК=90°-60°=30° .

Катет МК, лежащий против угла в 30°, равен половине гипотенузы, поэтому  МК=20:2=10 (см) .

Ответ:  Б)  МК=10 см .