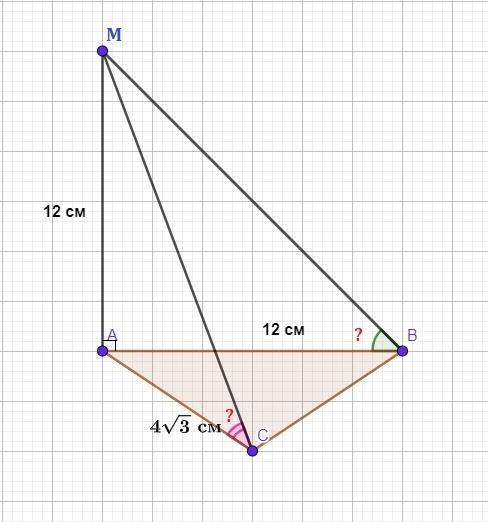
Пряма МА перпендикулярна до площини АВС, АВ=АМ=12 см, АС=4 см. Знайдіть кут, який утворює з площиною АВС пряма: 1) МВ; 2) МС.
см. Знайдіть кут, який утворює з площиною АВС пряма: 1) МВ; 2) МС.
Ответы
Ответ:
1) кут між площиною АВС та прямою МВ: ∠АВМ= 45°
1) кут між площиною АВС та прямою МС: ∠АСМ= 60°
Объяснение:
Пряма МА перпендикулярна до площини АВС, АВ=АМ=12 см, АС=4√3 см. Знайдіть кут, який утворює з площиною АВС пряма: 1) МВ; 2) МС.
- Пряма називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, яка лежить у цій площині.
МА⊥(АВС), АВ ∈ (АВС), АС ∈ (АВС) ⇒ МА⊥АВ, МА⊥АС.
- Кут між прямою та площиною — це кут між пряимою та її проекцією на цю площину.
1) ΔАМВ - прямокутний (∠А=90°), ⇒ АВ - проекція МВ на площину (АВС), ⇒ ∠АВМ - кут між прямою МВ та площиною (АВС).
АВ=АМ=12 см - за умовою, тому ΔАМВ - рівнобедрений.
У рівнобедреного трикутника кути при основі рівні, а сума гострих кутів прямокутного трикутника дорівнює 90°, маємо:
∠АВМ=∠АМВ= 90° : 2 = 45°.
2) ΔАМС - прямокутний (∠А=90°), ⇒ АС - проекція МС на площину (АВС), ⇒ ∠АСМ - кут між прямою МС та площиною (АВС).
АС=4√3 см, АМ=12 см - за умовою.
- Тангенсом гострого кута прямокутного трикутника є відношення його протилежного катета до прилеглого катета.
∠АСМ = 60°
#SPJ1