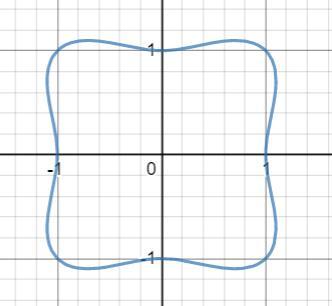
Сколько решений имеет данное уравнение?
x^4+y^4=x^2+y^2
a) 0
b) 2
c) Много
d) Нет решений
Ответы
Ответ:
с) Уравнение имеет много решений. (бесконечно много)
Пошаговое объяснение:
Перейдем к полярный координатам:
x=r cos φ, y= r sin φ
x⁴+y⁴=x²+y²
(rcos φ)⁴+(rsin φ)⁴=(rcos φ)²+(rsin φ)²
r⁴(cos⁴φ+sin⁴φ)=r²(cos²φ+sin²φ)
r⁴(cos⁴φ+sin⁴φ)=r²
r²(cos⁴φ+sin⁴φ)=1
Отметим, что для любого φ верно равенство
Доказывается это тождество возведением в квадрат основного тригонометрического тождества. Отметим также, что это выражение принимает значения, большие 1/2 (так как от 1 вычитается число, не большее, чем 1/2), то есть строго большие нуля, и на него можно делить, что мы делаем, когда вычисляем r.
Значит
- подставим это в выражение x и y:
Множество таких пар (x;y) является решением исходного уравнения, при этом в качестве φ можно взять любое действительное число. То есть таких пар бесконечно много.
PS: Для визуализации прилагаю картинку, на которой на координатной плоскости изображено множество таких пар. В задаче не требовалось строить такое изображение, поэтому опускаю детали, как это можно сделать без использования программ.
#SPJ1