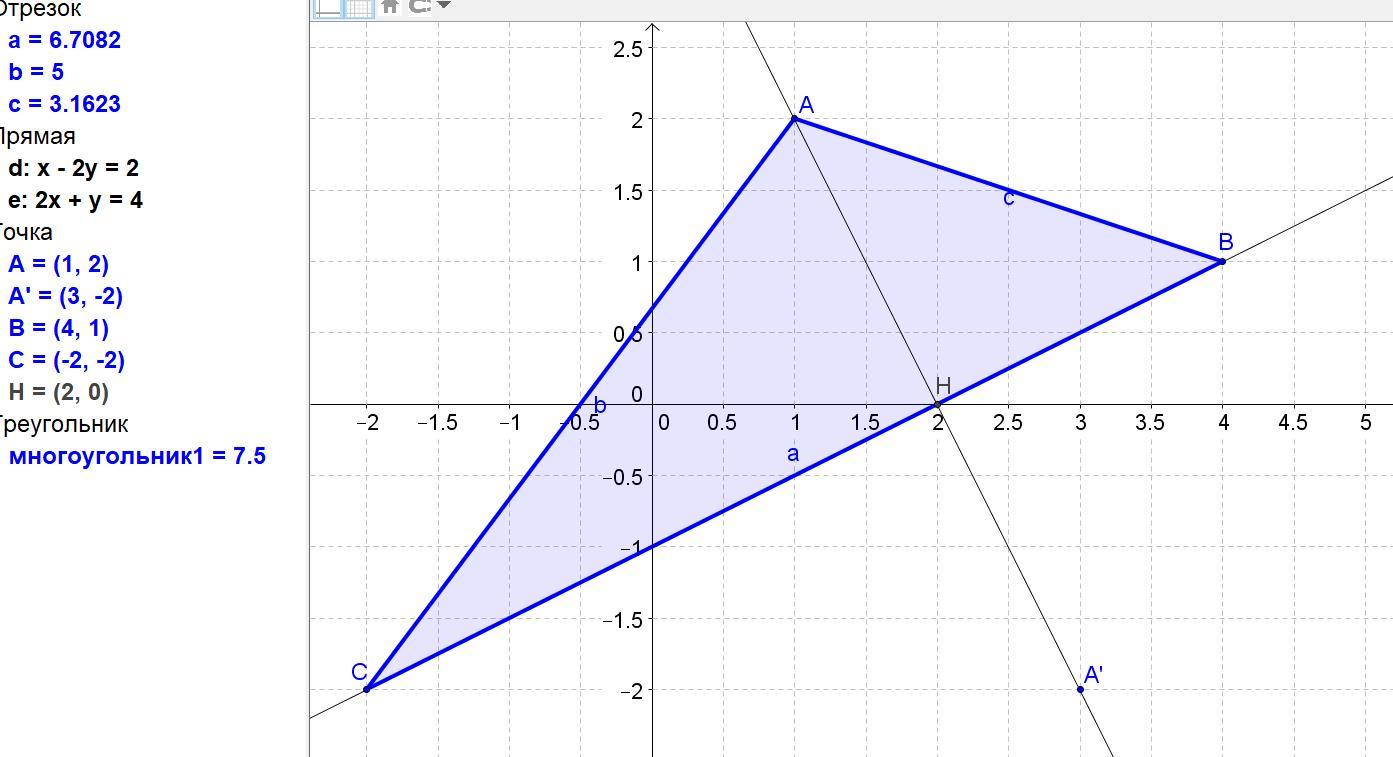
Задано три точки А, В, С. Знайти:
1) рівняння прямої ВС;
2) рівняння прямої, яка проходить через точку А паралельно до прямої ВС;
3) кут АВС;
4) рівняння та довжину медіани в трикутнику АВС, яка проведена з вершини А;
5) рівняння та довжину висоти в трикутнику АВС, яка проведена з вершини А;
6) знайти точку А1, яка симетрична точці А відносно прямої ВС.
1. A(1;2); B(4;1); C(-2;-2).
Ответы
1) Найти рівняння прямої ВС.
Находим вектор ВС.
ВС = (-2-4; -2-1) = (-6; -3).
Получаем уравнение прямой ВС:
ВС: (x – 4)/(-6) = (y – 1)/(-3) канонический вид.
-3х + 12 = -6у + 6,
3х – 6у - 6 = 0 или х – 2у - 2 = 0 общий вид.
у = (1/2)х – 1 с угловым коэффициентом.
2) Рівняння прямої в общем виде Ах + Ву + С = 0, яка проходить через точку А паралельно до прямої ВС, имеет коэффициенты А и В такие же, как и у прямой ВС: х – 2у + С = 0.
Подставим координаты точки А(1;2).
1 – 2*2 + С = 0, отсюда С = 1 – 1 = 3.
Получаем уравнение прямой х – 2у + 3 = 0.
3) Найти кут АВС. Точки A(1;2); B(4;1); C(-2;-2).
Векторы ВА = (1-4; 2-1) = (-3; 1), модуль равен √(9 + 1) = √10.
Векторы ВС = (-2-4; -2-1) = (-6; -3, модуль равен √(36 + 9) = √45 = 3√5.
cos B = (-3*(-6) + 1*(-3)) √10*3√5) = 15/(15√2) = 1/√2 = √2/2.
Угол В = arccos(√2/2) = 45 градусов.
4) Найти рівняння та довжину медіани в трикутнику АВС, яка проведена з вершини А.
Находим координаты точки М как середину стороны ВС.
М = (B(4;1) + C(-2;-2))/2 = (1; -1/2).
Находим вектор АМ.
АМ = (1-1; (-1/2)-2) = (0; -5/2).
Получаем уравнение прямой АМ:
АМ: (x – 1)/0 = (y – 2)/(-5/2) канонический вид.
(-5/2)х + (5/2) = 0, или х – 1 = 0 общий вид.
5) Найти рівняння та довжину висоти в трикутнику АВС, яка проведена з вершини А.
Уравнение перпендикулярной прямой.
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0, представляется уравнением
A(y-y1)-B(x-x1)=0.
Искомая высота перпендикулярна стороне ВС: х – 2у - 2 = 0.
Тогда уравнение перпендикуляра АН из точки А(1; 2) - будет иметь вид:
АН: 1(y – 2) – (-2)*(x – 1) = 0,
2x + y - 4 = 0.
Далее решение задачи может идти двумя путями: а) искать точку Н пересечения высоты и б) воспользоваться формулой определения расстояния от точки до прямой.
а) Находим координаты точки Н, решив систему с уравнениями прямых.
ВС: х – 2у - 2 = 0 х – 2у - 2 = 0
АН: 2x + y - 4 = 0|x(2) = 4x + 2y - 8 = 0
5x - 10 = 0,
x = 10/5 = 2, y = 4 – 2x = 4 – 2*2 = 0.
Точка Н(2; 0).
Вектор АН = (2 – 1; 0 – 2) = (1; -2).
Его модуль (длина) равен √(1² + (-2)²) = √(1 + 4) = √5.
б) Формула:
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|/√(A2 + B2).
Подставим в формулу данные:
d = |1·1 + (-2)·2 + (-2)|/√(|12 + (-2)2)= |1 - 4 – 2|/√(1 + 4) =
= 5/√5 = √5 ≈ 2,236068.
6) знайти точку А1, яка симетрична точці А відносно прямої ВС.
Используем координаты точки Н(2; 0) как середины отрезка АА1.
x(A1) = 2x(H) – x(A) = 2*2 – 1 = 3,
y(A1) = 2y(H) – y(A) = 2*0 – 2 = -2.
Точка А1(3; -2).