Предмет: Математика,
автор: irinaluka
Дана система неравенств: {
3 x- 2 y ≥ −6
3 x + y ≥ 3
x ≤ 3
А) Изобразите множество решений этой системы неравенств на плоскости.
Б) Найдите координаты вершин полученной фигуры.
C) Найдите решение, для которого значение изображения L = 2x + 2y
pushpull:
уточните вопрос С) просто дайте полный текст оригинала. не надо переводить на русский.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Для графического решения системы необходимо:
- Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
- Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
- Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
- Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.
3x- 2y ≥ −6
Строим график 3x- 2y = −6
В точке с абсциссой (0;0) получаем 0 > -6 следовательно, наша область решения располагается "ниже" графика 3x- 2y = −6.
3 x + y ≥ 3
Аналогично определяем область решения.
В точке (0; 0) получаем 0 > 6, что не верно. Следовательно, наша полуплоскость располагается "правее" графика 3x + y= 3.
x ≤ 3
Полуплоскость решения "левее" графика х = 3
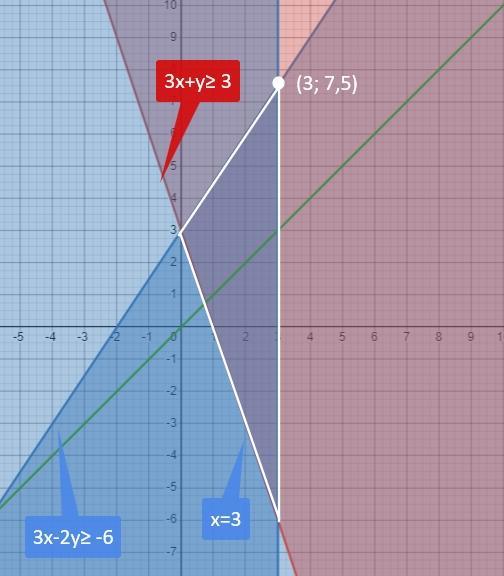
Таким образом, мы получили область решений, или "фигуру" на плоскости.
Б) координаты вершины (3; 7,5)
С) вопрос не понятен.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: petrovic20187
Предмет: Русский язык,
автор: albina19820107
Предмет: Русский язык,
автор: nierre
Предмет: Литература,
автор: lolacatlcat
Предмет: Биология,
автор: katyromashova2006