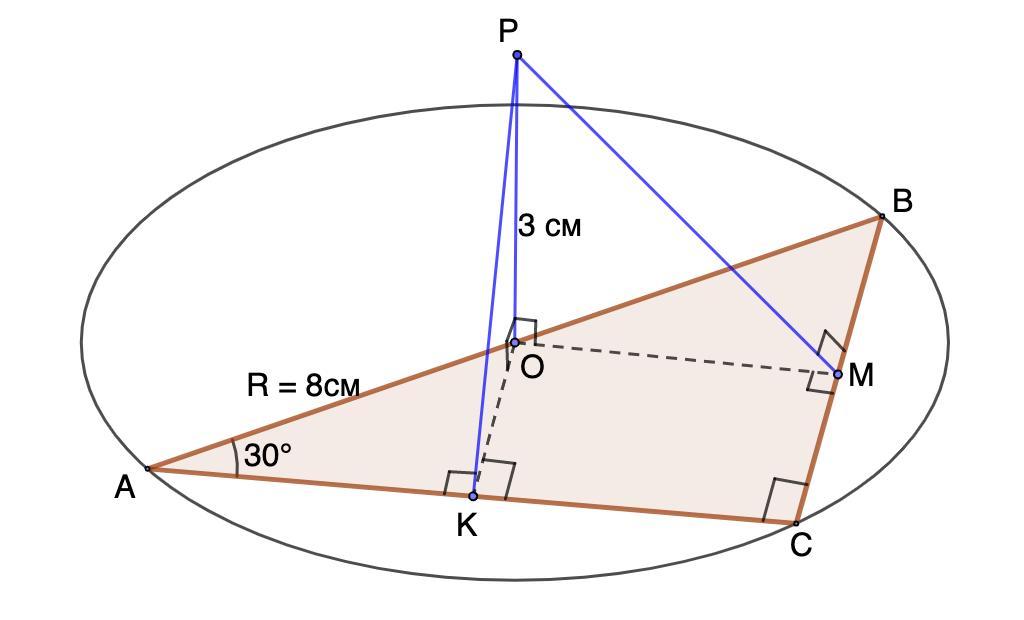
Предмет: Геометрия, автор: Silvestr54

Прямоугольный треугольник с острым углом 30° вписан в окружность радиуса 8 см. Из центра О окружности проведен перпендикуляр ОР к плоскости круга. Найти расстояние от точки Р до катетов треугольника, если ОР = 3 см
С решением пожалуйста.

BMW52: Могу без чертежа решить.

Silvestr54: Давайте

Ответы

Автор ответа: natalyabryukhova

Ответ:

Расстояния от точки Р до катетов треугольника АС и СВ соответственно равны 5 см и √57 см.

Объяснение:

Прямоугольный треугольник с острым углом 30° вписан в окружность радиуса 8 см. Из центра О окружности проведен перпендикуляр ОР к плоскости круга. Найти расстояние от точки Р до катетов треугольника, если ОР = 3 см.

Дано: ΔАВС - прямоугольный;

∠А = 30°;

Окр.О - описана около ΔАВС;

R = 8 см;

ОР ⊥ плоскости круга; ОР = 3 см.

Найти: расстояние от Р до катетов АС и СВ.

Решение:

Расстояние от точки до прямой - перпендикуляр, опкщенный из данной точки на данную прямую.

⇒ РК ⊥ АС; РМ ⊥ СВ.

⇒ Искомые отрезки РК и РМ.

Если прямая перпендикулярна плоскости, она перпендикулярна любой прямой, принадлежащей этой плоскости.

⇒ РО ⊥ ОМ; РО ⊥ ОК.

1. Рассмотрим ΔАВС - прямоугольный.

Окр.О - описанная.

Прямой вписанный угол опирается на диаметр.

⇒ АВ диаметр Окр.О.

АО = ОВ = 8 см.

Диаметр равен двум радиусам.

⇒ АВ = 8 · 2 = 16 (см)

∠А = 30°.

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ СВ = 16 : 2 = 8 см

По теореме Пифагора найдем АС:

АС² = АВ² - СВ² = 256 - 64 = 192

АС = √192 = 8√3 (см)

2. Рассмотрим ΔОРМ - прямоугольный.

РМ ⊥ СВ.

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

⇒ ОМ ⊥ СВ.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ ОМ || АС.

Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ ОМ - средняя линия ΔАВС.