Question

40 балів

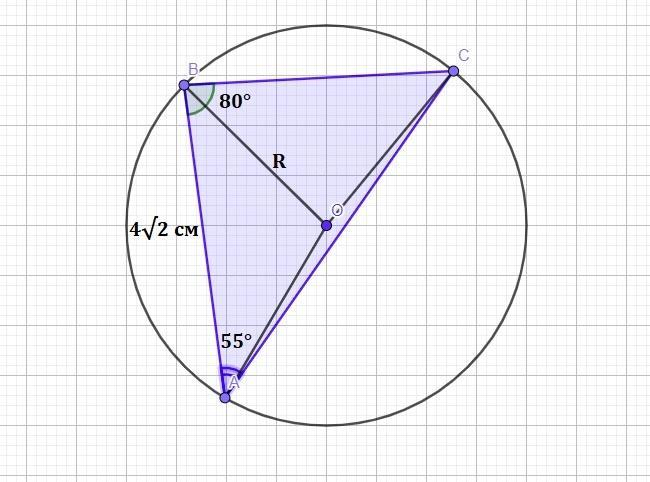
Сторона трикутника дорівнює 4√2 см, а прилеглі до неї кути рівні 80° і 55°. Знайдіть довжини дуг, на які ділять кути трикутника описане навколо нього коло.

Answer 1

Ответ:

∪СА =  32/9*π см

∪ВС = 22/9*π см

∪АВ =  2*π см

Пошаговое объяснение:

Сторона трикутника дорівнює 4√2 см, а прилеглі до неї кути рівні 80° і 55°. Знайдіть довжини дуг, на які ділять кути трикутника описане навколо нього коло.

• Довжина дуги кола радіуса R може бути обчислена за формулою:

$L = \dfrac{\pi Rn^\circ }{180^\circ}$

де L – довжина дуги; n° – градусна міра дуги.

• Градусна міра центрального кута дорівнює градусній мірі дуги,на яку він спирається.

1) Так як сума кутів трикутника дорівнює 180°, то ∠С=180°-∠А-∠В=180°-55°-80°=45°

2) За теоремою синусів знайдемо радіус R описаного кола:

AB/sin∠C = 2*R

R = AB / 2* sin 45° = 4√2 / (2*(√2/2)) = 4√2 / √2 = 4 cм.

3) Центральний кут у два рази більше за   вписаний. Тому:

∠СОА = 2*∠В=2*80°=160°,

∠СОВ=2*∠А=2*55°=110°,

∠АОВ=2*∠С=2*45°=90°

∪СА = ∠СОА*R*π/180° = 160° *4*π/180° = 32/9*π см

∪ВС = ∠СОВ*R*π/180° = 110° *4*π/180° = 22/9*π см

∪АВ = ∠АОВ*R*π/180° = 90° *4*π/180° = 2*π см

#SPJ1