Предмет: Математика,
автор: ksuhalavrinenko1609
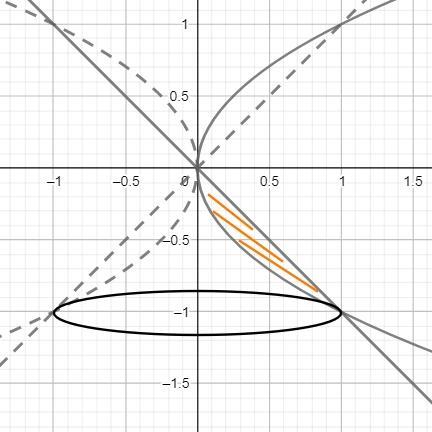
Об’єм тіла, утвореного обертанням навколо осі 0y фігури, яка обмежена лініями
y²=x, y= -x
Ответы
Автор ответа:
2
Ответ:
Объем тела равен ед³
Пошаговое объяснение:
Формула для вычисления объема
Делаем чертеж, получаем фигуру и пределы интегрирования.
Выразим функции в виде х²(y).
y₁²=x₁ x₁² = (y₁)⁴
y₂ = -x₂ x₂² = (-y₂)²
Объем нашего тела - это объем конуса (y₂=-x₂) минус объем параболоида (y₁²=x₁ )
Рассчитаем объем
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: maria0125
Предмет: Окружающий мир,
автор: ГошаОганян
Предмет: Английский язык,
автор: ainkafedorova06
Предмет: Литература,
автор: idontlikeexams78