Предмет: Алгебра,
автор: Sasha211004
Упростить выражение 2log2(7)+ log5 (75) - log5 (3)
Приложения:
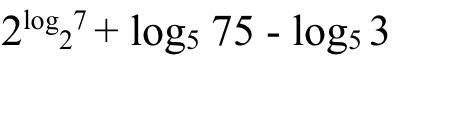
Ответы
Автор ответа:
3
Упростить выражение 2log2(7)+ log5(75) - log5(3).
Ответ:
9
Объяснение:
Свойства логарифмов, которые будут использоваться:
Похожие вопросы
Предмет: Українська мова,
автор: vladOMG2
Предмет: Русский язык,
автор: барият14
Предмет: Русский язык,
автор: dianayantimirova
Предмет: Алгебра,
автор: ilua1403
Предмет: Обществознание,
автор: ХАТИКОCSGO
=log5 (75/3)=log5 (25) =2 ;
7+2=9