Question

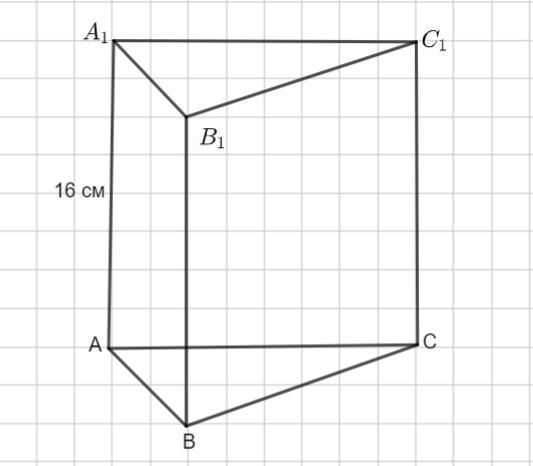
В прямій трикутній призмі сторони основи відносяться як 17 : 10 : 9, а бічне ребро дорівнює 16 см. Повна поверхня цієї призми 1440 см2. Знайдіть її бічну поверхню.

Answer 1

Ответ:

Площадь боковой поверхности призмы равна 1152 см².

Пошаговое объяснение:

Дана прямоугольная призма $ABC A_{1} B_{1} C_{1}$. Стороны основания

АС: ВС: АВ = 17: 10: 9. Боковое ребро равно 16 см. Полная поверхность призмы равна 1440 см². Надо найти площадь боковой поверхности призмы.

Пусть одна часть будет х см. Тогда стороны основания будут

АС=17х см ВС=10х см,  АВ = 9х см.

Найдем площадь данного треугольнике по формуле Герона:

$S= \sqrt{p(p-a)(p-b)(p-c) } ,$ где

a,b,c- стороны треугольника, а  p - полупериметр.

$p=\dfrac{17x+10x+9x}{2} =\dfrac{36x}{2} =18x;\\\\S= \sqrt{18x\cdot(18x-17x)(18x-10x)(18x-9x) } =\sqrt{18x\cdot x\cdot 8x \cdot9x } =\\\\=\sqrt{9x\cdot x \cdot 16x\cdot 9x } =9x\cdot 4x=36x^{2}$

Площадь полной поверхности равна сумме боковой поверхности и сумме двух оснований.

Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы. Так как  призма прямая, то боковое ребро является высотой призмы.

Тогда площадь боковой поверхности будет равна

$S= (17x+10x+9x)\cdot16=36x\cdot 16$

Тогда площадь полной поверхности будет равна

$2\cdot 36x^{2} +36x\cdot16=1440|: 72;\\x^{2} +8x-20=0;\\D= 8^{2} -4\cdot1\cdot (-20) = 64+80=144=12^{2} \\\\x{_1}= \dfrac{-8-12}{2} =\dfrac{-20}{2} =-10;\\\\x{_2}= \dfrac{-8+12}{2} =\dfrac{4}{2} =2.$

Условию задачи удовлетворяет только положительное значение, то х=2.

Найдем  площадь боковой поверхности призмы

$S=36x\cdot 16=36\cdot2\cdot 16=1152$

Значит, площадь боковой поверхности призмы равна 1152 см².

#SPJ1