Question

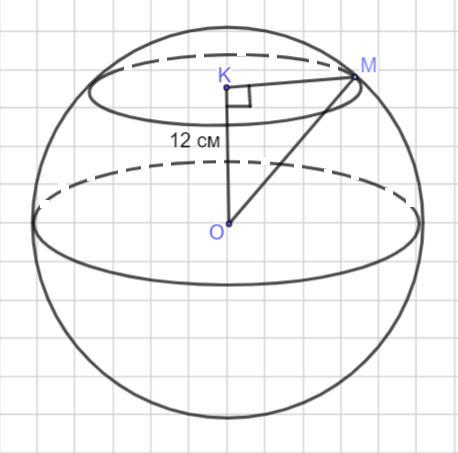
На відстані 12 см від центра кулі проведено площину. Площа утвореного перерізу
дорівнює 64π см2
Знайти радіус кулі.

Answer 1

Ответ:

Радиус шара равен 4√13 см.

Объяснение:

Дан шар. На расстоянии 12 см от центра шара проведена плоскость . Площадь сечения равна 64π см². Надо найти радиус шара.

Любое сечение будет круг. Площадь круга равна 64π см². Площадь круга определяется по формуле:

$S=\pi r^{2}$

Тогда

$\pi r^{2} =64\pi ;\\r^{2} =64;\\r=8$

Значит, радиус сечения равен 8 см. То есть КМ = 8см.

Рассмотрим ΔКОМ - прямоугольный.

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$OM^{2} =OK^{2} +KM^{2} ;\\OM = \sqrt{OK^{2} +KM^{2}} ;\\OM=\sqrt{12^{2} +8^{2} } =\sqrt{144+64} =\sqrt{208} =\sqrt{4\cdot 4\cdot13} =4\sqrt{13}$

Значит, радиус шара равен 4√13 см.

#SPJ1