Question

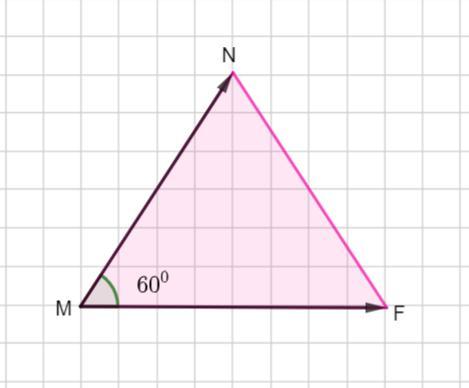
У правильному трикутнику MNF із стороною NF = 5 см, побудовано вектори MN та MF. Знайти скалярний добуток цих векторів.

Answer 1

Ответ:

$\vec{MN}\cdot \vec{MF}=12,5$

Объяснение:

Дан правильный ΔMNF  со стороной NF равной 5 см.

Построим векторы $\vec{MN}$  и  $\vec{MF}$и найдем скалярное произведение этих векторов.  

Скалярное произведение векторов равно произведению длин этих векторов на косинус угла между векторами .

Так как ΔMNF  - правильный, то все стороны равны 5 см и все углы по 60 °.

Тогда длины векторов равны 5, а угол между данными векторами ∠М = 60 °.

Тогда получим

$\vec{MN}\cdot \vec{MF}= |\vec{MN}|\cdot |\vec{MF}|\cdot cos M;\\\vec{MN}\cdot \vec{MF}=5\cdot5\cdot cos60^{0} =25\cdot \dfrac{1}{2} =12,5$

Скалярное произведение данных векторов равно 12,5.

#SPJ1