Question

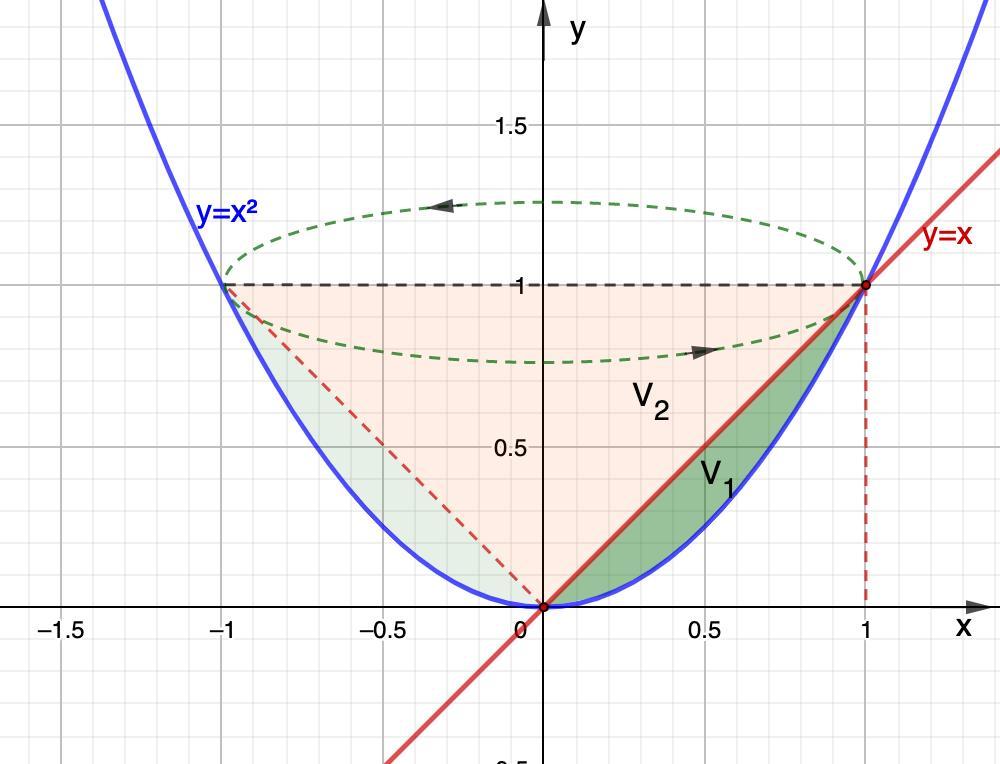
Обчислити об'єм тіла, утвореного обертанням фігури, обмеженої графіками наступних функцій навколо вісі OY.y = x^2, y = x

Answer 1

Ответ:

Объем тела, образованного вращением фигуры, ограниченной графиками функций y = x² и y = x вокруг оси OY равен $\displaystyle \frac{1}{6}\pi$ ед.³.

Объяснение:

Вычислить объем тела, образованного вращением фигуры, ограниченной графиками следующих функций вокруг оси OY:

y = x², y = x.

Объем тела вращения найдем по формуле:

$\displaystyle \boxed {V_{Oy}=\pi \int\limits^d_c {(x_2^2(y)-x_1^2(y))} \, dy }$

Выполним построение фигуры.

Искомый объем будет равен разности объемов параболоида, образованного вращением кривой х² = у и конуса, образованного вращением прямой х = у.

Найдем точки пересечения графиков.

Решим систему:

$\displaystyle \left \{ {{y=x^2} \atop {y=x}} \right.$

x² = x

x(x - 1) = 0

x = 0;   x = 1

y(0) = 0;   y(1) = 1

⇒ пределы интегрирования с = 0; d = 1.

x₂² = y;   x₁² = y²    

Для вычисления нам понадобится формула Ньютона-Лейбница:

$\displaystyle \boxed {\int\limits^b_a {f(x)} \, dx =F(b)-F(a)}$

Теперь можем вычислить объем:

$\displaystyle V_1 =\pi \int\limits^1_0 {(y-y^2)} \, dy=\pi \left(\frac{y^2}{2}-\frac{y^3}{3}\right)\bigg|^1_0=\\ \\ =\pi \left(\frac{1}{2}-\frac{1}{3}-0\right)=\frac{3-2}{6} \pi =\frac{1}{6}\pi$

Объем тела, образованного вращением фигуры, ограниченной графиками функций y = x² и y = x вокруг оси OY равен $\displaystyle \frac{1}{6}\pi$ ед.³.

#SPJ1