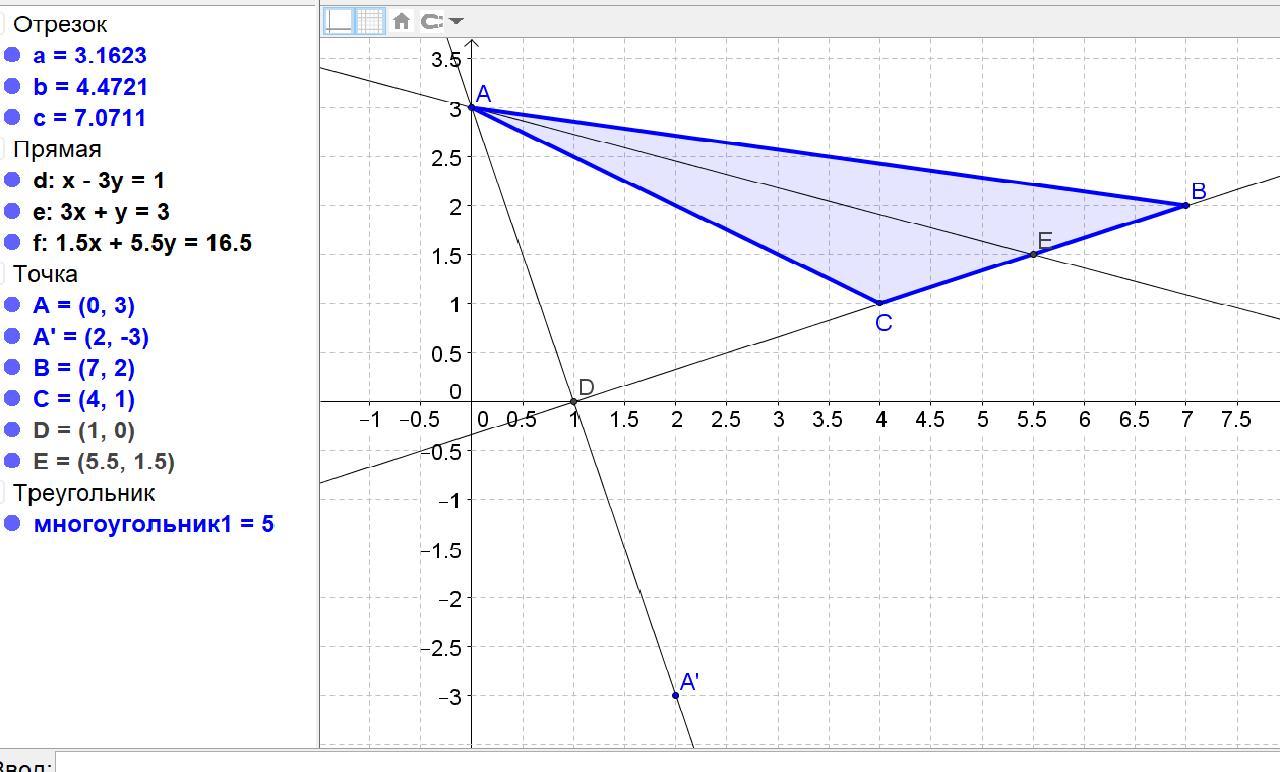
Дано точки А(0;3) В(7;2) С(4;1) задано точки А, B, C знайти 1) рівняння прямої ВС; 2) рівняння прямої яка проходить через точку А паралельно до прямої ВС; 3)кут АВС; 4) рівняння та довжину медіани в трикутнику АВС яка проведена з вершини А; 6)знайти точку А1 яка симетрична точці А відносно прямої ВС.
Ответы
Дано точки А(0;3), В(7;2), С(4;1).
Знайти 1) рівняння прямої ВС;
Находим уравнение стороны ВС по точкам В(7;2), С(4;1)
Вектор ВС = ((4-7); 1-2))) = (-3; -1).
Уравнение ВС: (х - 7)/(-3) = (у - 2)/(-1)
-x + 7 = -3y + 6
x - 3y - 1 = 0 или y = (1/3)x – (1/3).
2) рівняння прямої яка проходить через точку А паралельно до прямої ВС;
Уравнение этой прямой x - 3у + C = 0.
Подставим координаты точки А(0; 3).
0 – 3*3 + C = 0.
Отсюда С = 9.
Получаем уравнение x - 3у + 9 = 0.
3)кут АВС;
Находим векторы ВА и ВС.
Вектор ВА = (0-7; 3-2) = (-7; 1). Его модуль равен √(49 + 1) =√50 = 5√2.
Вектор ВС == (4-7; 1-2) (-3; -1). Его модуль равен √9 + 1) = √10.
cos B = (-7*(-3) + 1*(-1)/(5√2*√10) = 20/(10√5) = 2/√5.
Угол В = arccos(2/(√5)) = 0,463648 радиан или 26,56505 градуса.
4) рівняння та довжину медіани в трикутнику АВС яка проведена з вершини А;
Находим координаты точки Е как середины стороны ВС.
Точки А(0; 3), В(7; 2), С(4; 1).
Е(7+4)/2; (2+1)/2) = (5,5; 1,5).
Вектор АЕ = ((0-5,5); (3-1,5))) = (-5,5; 1,5).
Уравнение АЕ: (х – 0)/(-5,5) = (у - 3)/(1,5) или х/(-11) = (у - 3)/3 .
Это в каноническом виде.
Оно же в общем виде:
3х = -11у + 33,
3х + 11у – 33 = 0.
И в виде уравнения с угловым коэффициентом у = (-3/11)х + 11.
5) знайти точку А1, яка симетрична точці А відносно прямої ВС.
Используем уравнение стороны ВС: y = (1/3)x – (1/3).
У прямой, перпендикулярной к прямой BC, угловой коэффициент равен к = -1(1/3) = -3.
Тогда уравнение перпендикуляра у = -3х + b.
Подставим координаты точки A(0; 3).
3 = (-3)*0 + b, отсюда b = 3.
Получаем уравнение высоты АD:
y = -3х + 3 или в общем виде 3х + у – 3 = 0.
Находим точку пересечения прямой ВС и высоты к ней.
ВС: x - 3y - 1 = 0 x - 3y - 1 = 0
АD: 3х + у – 3 = 0|x3 = 9х + 3у – 9 = 0.
10x -10 = 0.
x = 10/10 = 1, y = 3 – 3x = 3 – 3*1 = 0.
Точка пересечения D(1; 0).
Теперь ищем точку А1, симметричную точке А относительно прямой ВС.
x(A1) = 2x(D) – x(A) = 2*1 – 0 = 2.
y(A1) = 2y(D) – y(A) = 2*0 – 3 = -3.
Точка А1(2; -3).