Предмет: Алгебра,
автор: Nim213
Помогите, очень срочно.
Приложения:
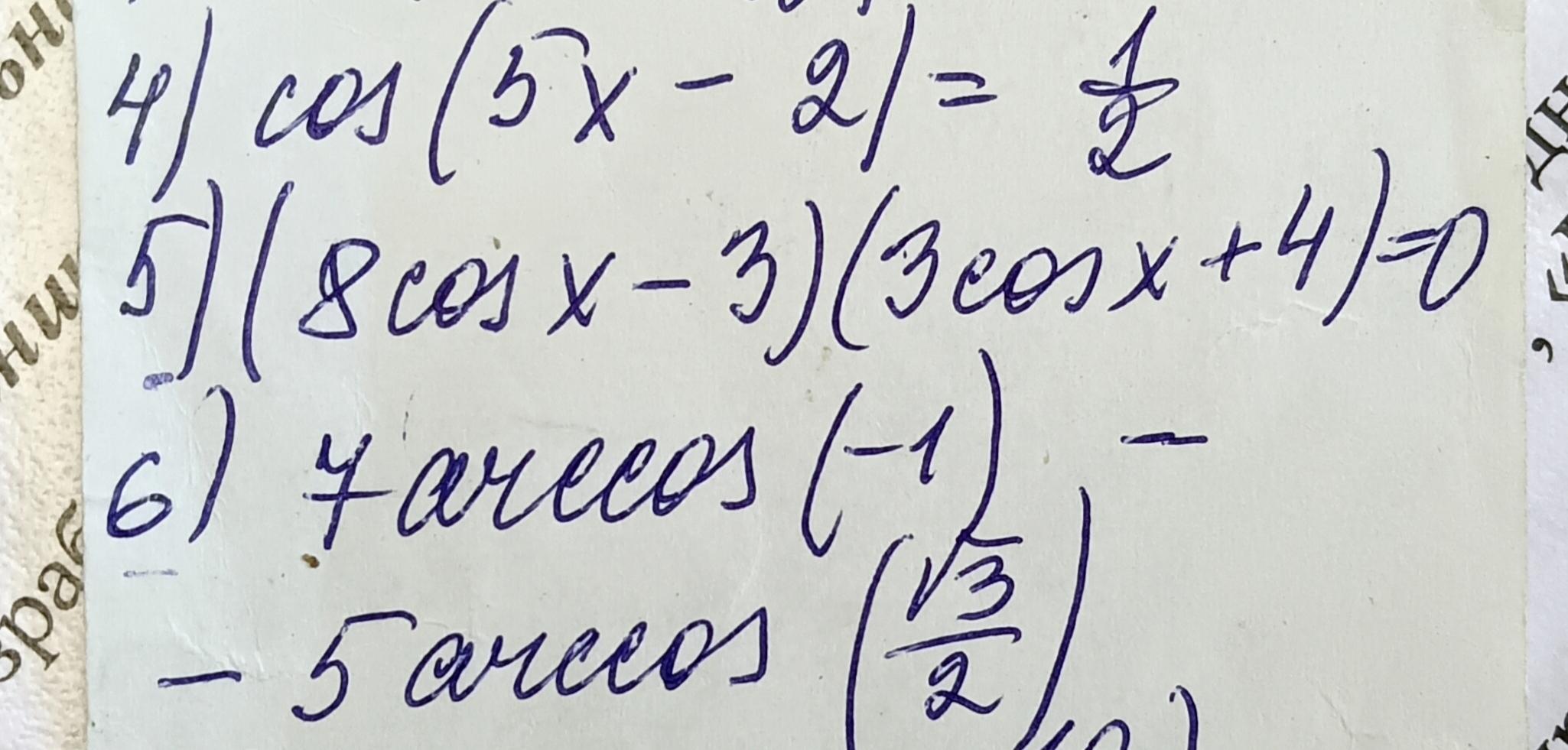
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Приложения:

Автор ответа:
1
Ответ:
решение смотри на фотографии
Приложения:


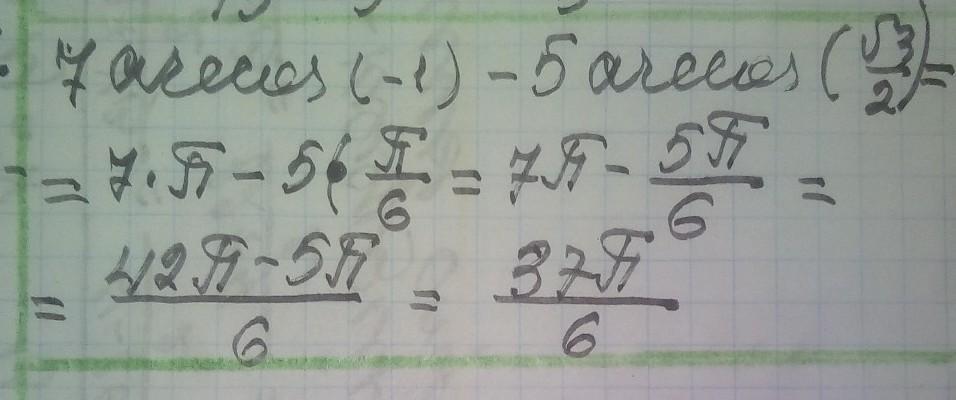
Похожие вопросы
Предмет: Английский язык,
автор: bugaets16
Предмет: Русский язык,
автор: Stasy0608
Предмет: Русский язык,
автор: vgheorghevna
Предмет: Алгебра,
автор: krike
Предмет: Обществознание,
автор: kbviknik