Предмет: Геометрия,
автор: SS6129
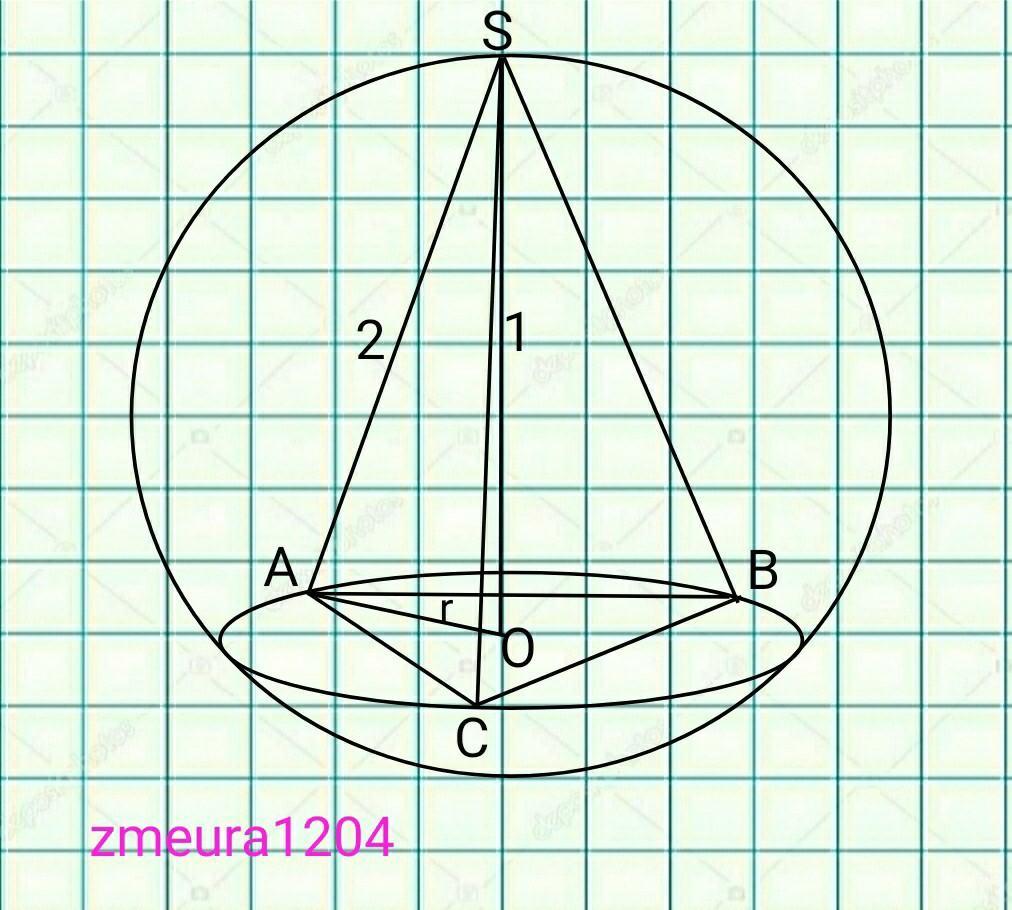
Найдите радиус сферы, описанной около правильной треугольной пирамиды, боковые ребра которой равны 2 см, а высота равна 1 см.
Anythingelsesyou:
Hi!Hi!
Ответы
Автор ответа:
1
Ответ:
2 см
Объяснение:
∆SAO- прямоугольный треугольник
По теореме Пифагора:
АО=√(SA²-SO²)=√(2²-1²)=√(4-1)=√3см
АО- радиус описанной окружности вокруг треугольника ∆АВС.
Из формулы r=a/√3, где а-сторона треугольника.
АО=АВ/√3; найдем сторону треугольника.
АВ=АО*√3=√3*√3=3см
Формула сферы:
R=(3*SO²+AB²)/(6*SO)
R=(3*1²+3²)/(6*1)=12/6=2см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: bugaets16
Предмет: Окружающий мир,
автор: danil1702
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: nglusheko
Предмет: Математика,
автор: evgesha0359