Предмет: Алгебра,
автор: nikad38
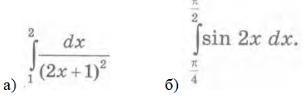
Обчислити визначений інтеграл
Приложения:
Ответы
Автор ответа:
2
дивіться фото...........................
Приложения:
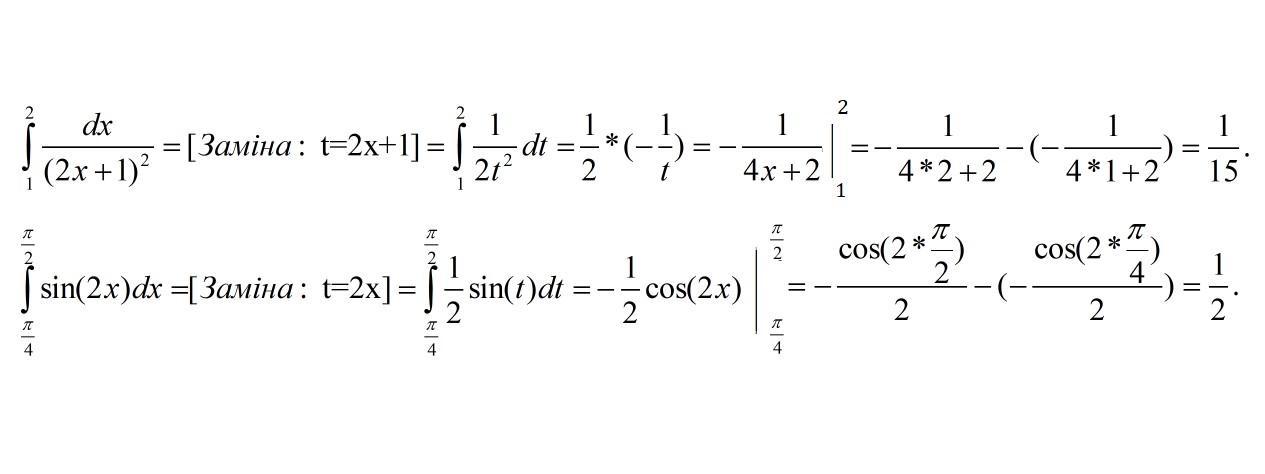
Автор ответа:
2
Решение.
Подведение под знак дифференциала. Выделяем дифференциал функции, которая является внутренней для подынтегральной функции .
Похожие вопросы
Предмет: Русский язык,
автор: поля761
Предмет: Английский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: элиночка2006
Предмет: Математика,
автор: anna030304
Предмет: Математика,
автор: gavanna2006