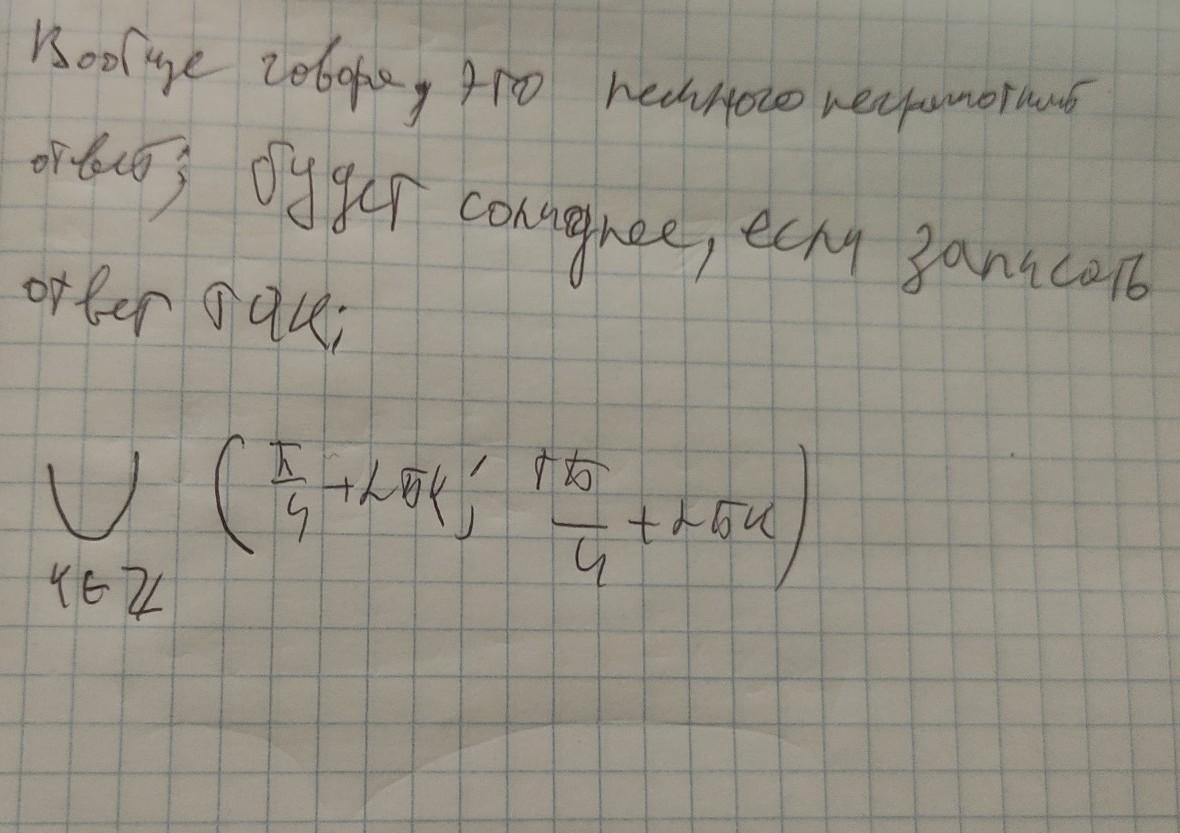Question

Решите неравенство введением вспомогательного (дополнительного) угла:

$\sin(x) > \cos(x)$

​

Answer 1

Ответ:

C. π/4+2πk<x<5π/4+2πk; kЄZ.

Объяснение:

sin(x)>cos(x);

можно перенести cos(x) в лево

sin(x)-cos(x)>0;

можно вынести √(2)

√2(1/√2 *sin(x)-1/√2 *cos(x))>0

1/√2 можно представить как sin(π/4) и как cos(π/4)

√2(sin(π/4)*sin(x)-cos(π/4)*cos(x))>0;

можно сократить на √2

sin(π/4)*sin(x)-cos(π/4)*cos(x)>0;

можно вынести -1

-1(cos(π/4)*cos(x)-sin(π/4)*sin(x))>0

по формуле косинуса суммы

-1(cos(π/4+x)>0

можно сократить на -1, но так как это отрицательное число - знак неравенства поменяется.

cos(π/4+x)<0

так как косинус отрицательный от 90 до 270° и от -270 до -90, то.

π/2+2πk<π/4+x<3π/2+2πk

-3π/2+2πk<π/4+x< -π/2+2πk

То

π/2-π/4+2πk<x<3π/2-π/4+2πk

-3π/2-π/4+2πk<x< -π/2-π/4+2πk

Значит

π/4+2πk<x<5π/4+2πk

-7π/4+2πk<x<-3π/4+2πk

а это одно и тоже

Ответ: π/4+2πk<x<5π/4+2πk, kЄZ(Целое число).

Ответ.С)

Answer 2

Ответ: С).

Решение на фотографии 1. На фотографии 2 небольшое примечание, в школе об этом не говорят