Предмет: Геометрия,
автор: NasAnishenko777
Дана окружность радиуса 6 с центром в точке O. Через точку A, расположенную вне окружности, и точку O проведена прямая, пересекающая окружность в точках P и Q. Найдите длину AQ, если известно, что длина касательной AB, проведённой к данной окружности, равна 8
Ответы
Автор ответа:
0
По условию: РО = 6 ; АВ = 8
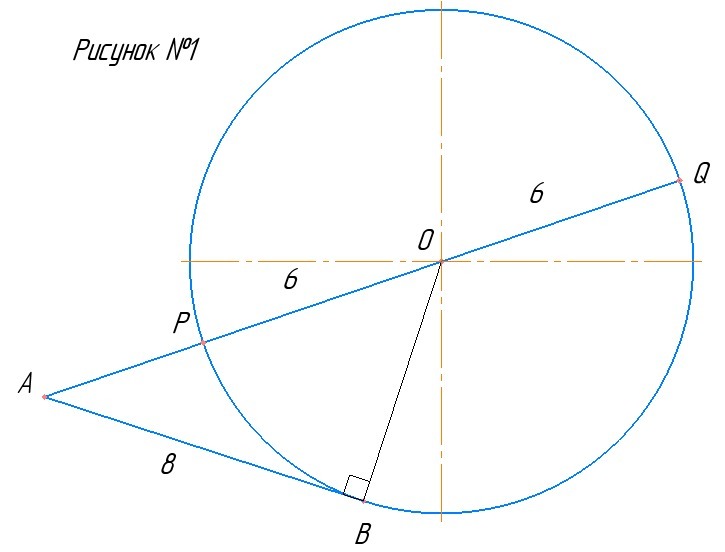
1) Рассмотрим случай, когда точка Р лежит между точкой А и О (см. рисунок №1)
Треугольник ОАВ - прямоугольный, т.к. радиус перпендикулярен к касательной в точке касания. OB = OP = 6
Тогда по теореме Пифагора

Тогда

Ответ: AQ = 16
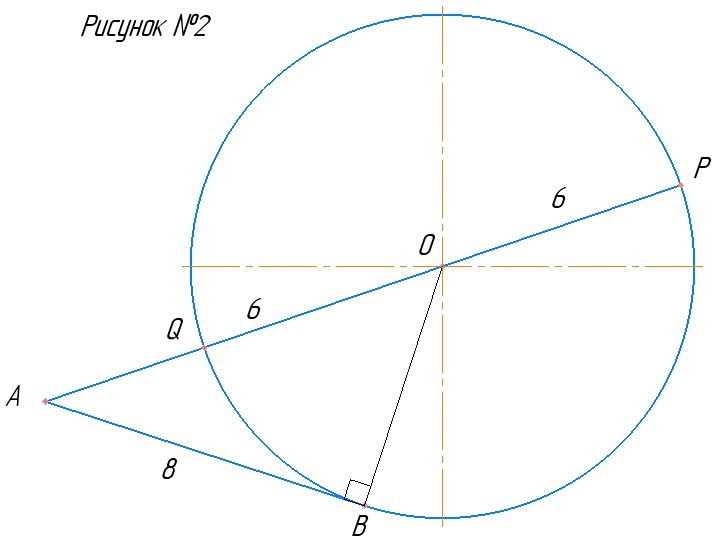
2) Рассмотрим случай, когда точка Q лежит между точкой А и О (см. рисунок №2)
OA = 10 (см. решение выше), тогда

Ответ: AQ = 4
1) Рассмотрим случай, когда точка Р лежит между точкой А и О (см. рисунок №1)
Треугольник ОАВ - прямоугольный, т.к. радиус перпендикулярен к касательной в точке касания. OB = OP = 6
Тогда по теореме Пифагора
Тогда
Ответ: AQ = 16
2) Рассмотрим случай, когда точка Q лежит между точкой А и О (см. рисунок №2)
OA = 10 (см. решение выше), тогда
Ответ: AQ = 4
Приложения:
Похожие вопросы
Предмет: История,
автор: libichoeva
Предмет: Физика,
автор: urakovabrorxon46
Предмет: Математика,
автор: ashirova647
Предмет: Физика,
автор: iskarugby98
Предмет: Алгебра,
автор: AlinaGreys