Предмет: Геометрия,
автор: irinashevchenk3606
Прямая пересекает точки А(1;3;2) и B(3;1;6)
Найдите площадь Треугольника образованного этой прямой и осями координат
Ответы
Автор ответа:
1
Прямая пересекает точки А(1;3;2) и B(3;1;6).
Найдите площадь треугольника, образованного этой прямой и осями координат.
Находим вектор АВ = (3-1; 1-3; 6-2) = (2; -2; 4).
Уравнение прямой АВ: (x - 1)/2 = (y – 3)/(-2) = (z – 2)/4.
Оно же в параметрическом виде:
x = 2t + 1,
y = -2t + 3,
z = 4t + 2.
Если принять z = 0, то прямая пересекает плоскость хОу.
4t + 2 /4 = -1/2.
Подставим значение t в уравнения прямой:
x = 2*(-1/2) + 1 = -1 + 1 = 0,
y = -2(-1/2) + 3 = 1 + 3 = 4.
Как видим, прямая пересекает ось Оу в точке (0; 4; 0).
Проверяем пересечение с плоскостью хОz. При этом у = 0.
-2t + 3 = 0,
t = -3/(-2) = 3/2.
x = 2*(3/2) + 2 = 5,
z = 4*(3/2) + 2 = 8.
Поэтому прямая больше не пересекает осей координат, и заданная задача не имеет смысла.
Приложения:
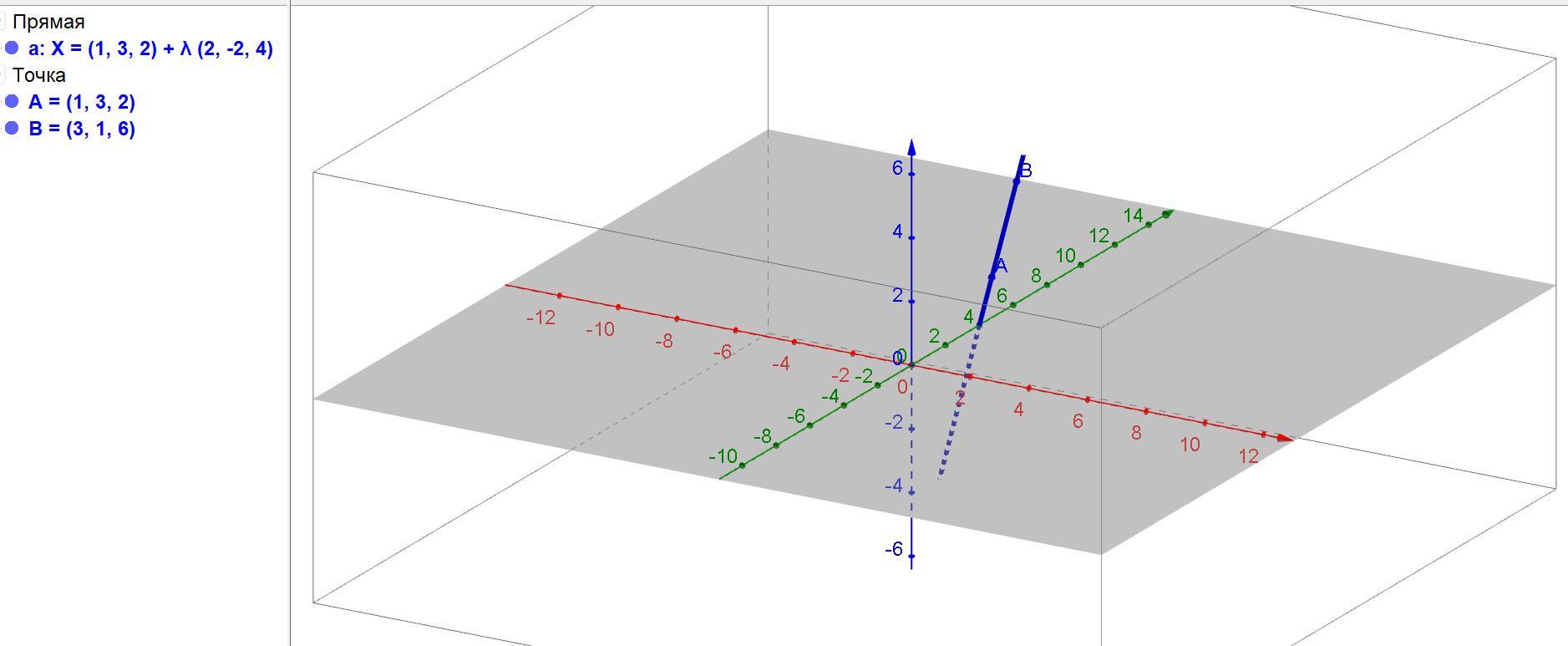
muratgamechanel:
Что за приложение для построения графика прямых с аппликатой
или сайт
География
Геогебра.
Благодарю
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Немецкий язык,
автор: ПeTyx
Предмет: Қазақ тiлi,
автор: andrey63587
Предмет: География,
автор: artem2222280
Предмет: Химия,
автор: ameriwether