Предмет: Алгебра,
автор: tkacenkoalina40
Обчислити визначений інтеграл безпосередньо.
Приложения:
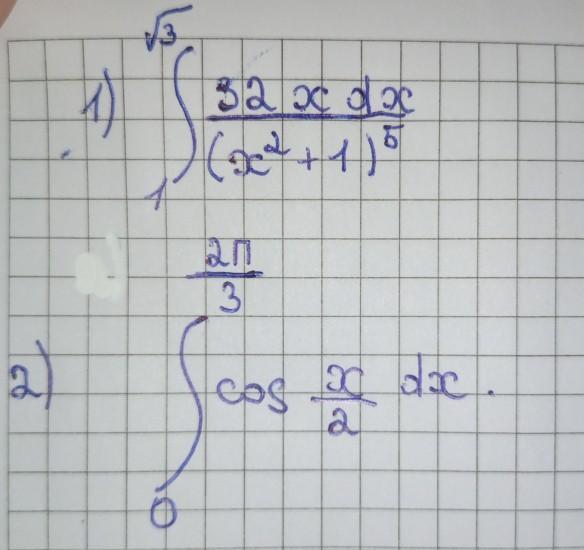
Ответы
Автор ответа:
0
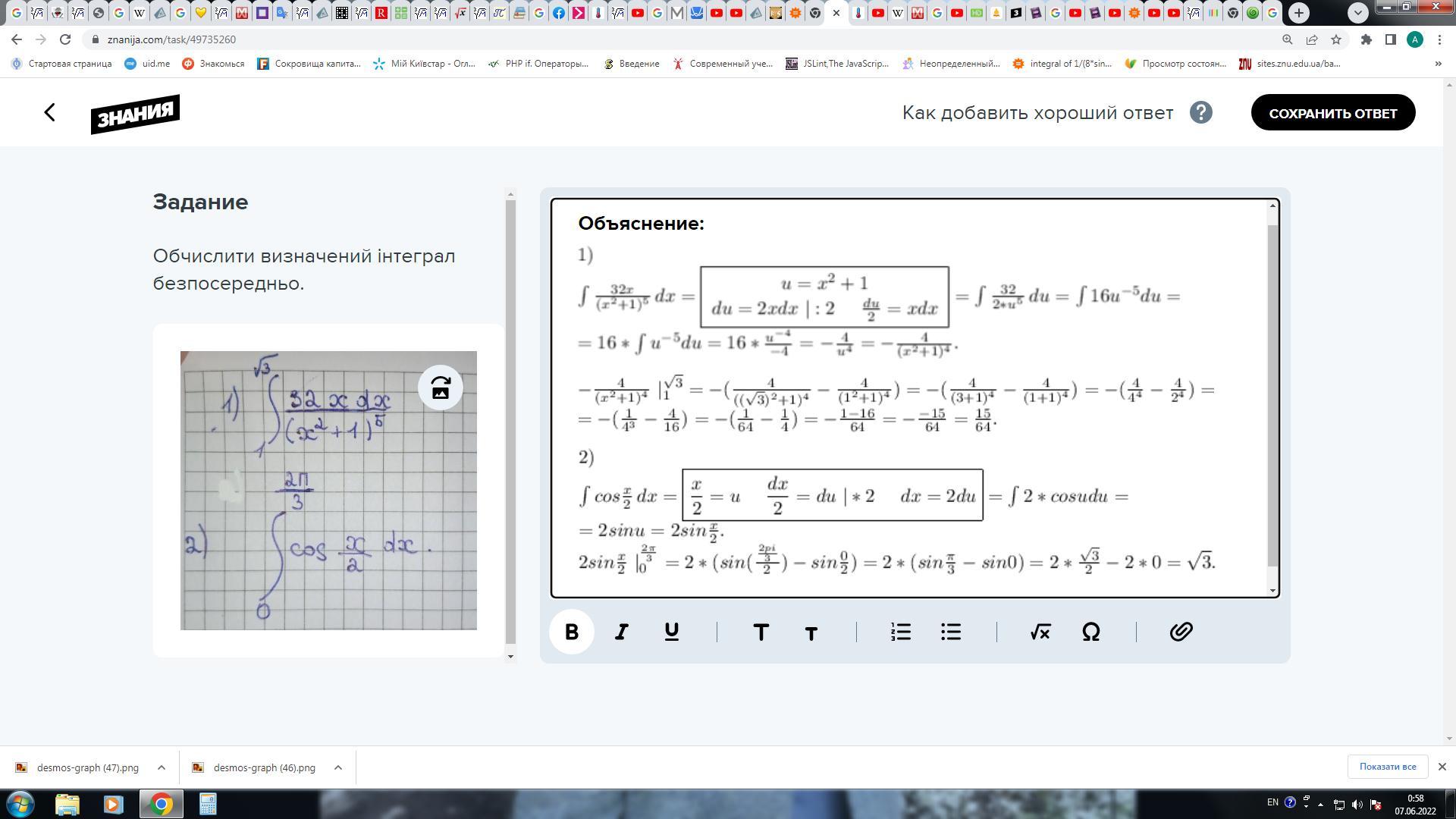
Объяснение:
Приложения:
tkacenkoalina40:
Здравствуйте можете пожалуйста помочь с алгеброй задания на странице
Похожие вопросы
Предмет: Русский язык,
автор: нелля16
Предмет: Окружающий мир,
автор: Элина11111111008
Предмет: Русский язык,
автор: sereginapolina
Предмет: История,
автор: Mariacat19