Предмет: Алгебра,
автор: kosmos787
На графіку функції y=x+1/x+3 знайдіть точки, у яких дотична паралельна прямій y=2x+1
Приложения:
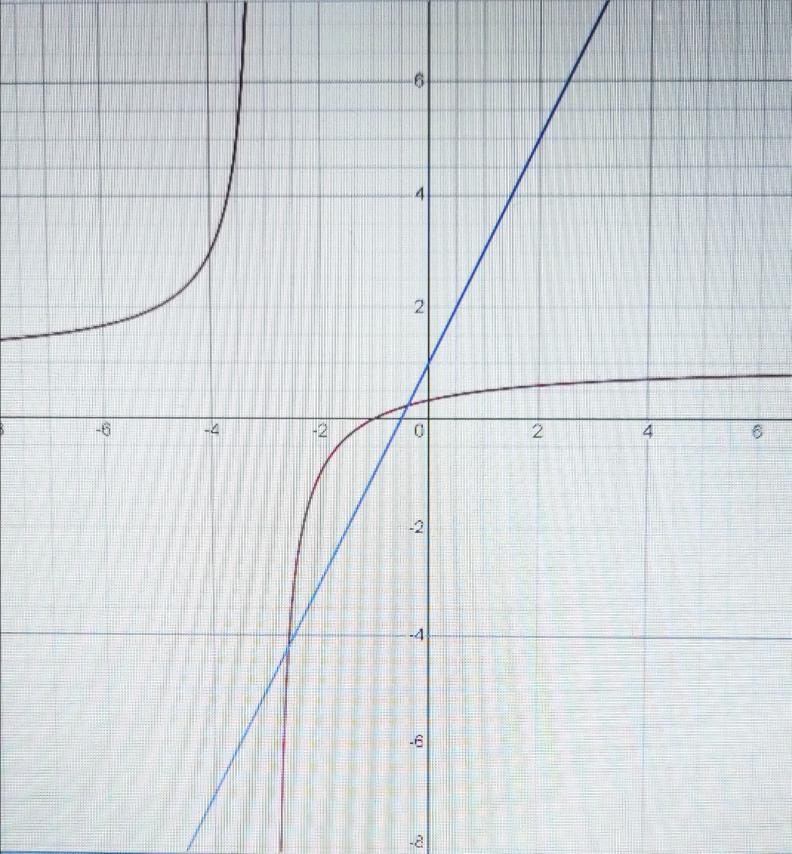
Ответы
Автор ответа:
1
Ответ:
(-4;3) і (-2;-1)
Объяснение:
Якщо дотична паралельна прямій у=2х+1, то її коефіцієнт дорівнює коефіцієнту цієї прямої, тобто k=2
Використаємо геометричний зміст похідної:
f'(x0) = k
у'=
Прирівняємо до k
Поділимо обидві частини рівняння на 2
За теоремою Вієта:
х1 = -4
х2 = -2
Щоб знайти точки, нам треба замість х підставити знайдені значення
х1:
Отже, перша точка (-4;3)
х2:
Отже, друга точка (-2;-1)
Похожие вопросы
Предмет: Русский язык,
автор: Влад45555
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: lorunshik
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: hegghdjd