Question

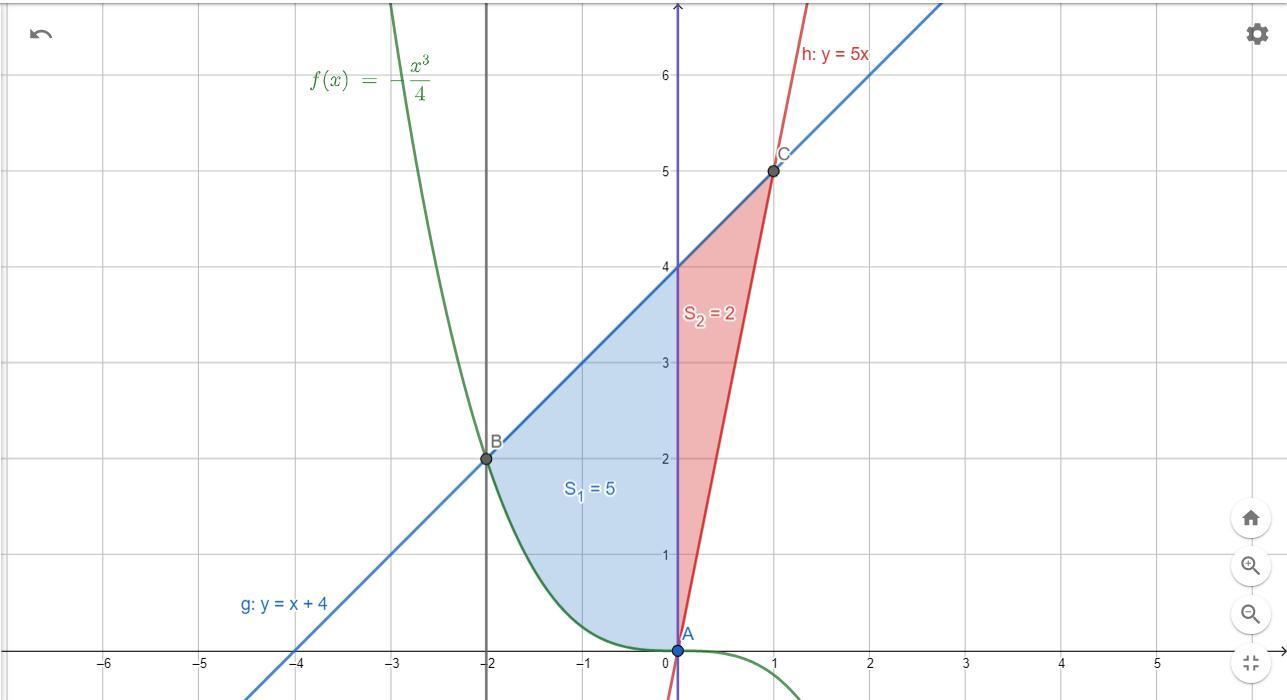
Вычислите площадь фигуры, ограниченной заданными линиями: y = - 1/4 х3, y=4+x, y=5x

Answer 1

Ответ: Площадь фигуры, ограниченной заданными линиями:          y = - x³/4  , y=4+x ,  y=5x   равна 7 (ед)²

Объяснение:

Вычислите площадь фигуры, ограниченной заданными линиями :

y = - x³/4  , y=4+x ,  y=5x

Формула Ньютона - Лейбница

Для непрерывной функции f(x) :

$\displaystyle \boldsymbol{ \int\limits^a_b {f(x)} \, dx = F(x) \bigg | ^ a_b= F(a) - F(b)}$  ,  где  F(x)  - первообразная для функции  f(x)

Найдем точки пересечения графиков

-x³/4  = 4 + x

x³ + 4x + 16 =0

x = - 2  

                                           

x + 4 = 5x  

4x = 4

x = 1

                                           

-x³/4  = 5x

x = 0  

Проведем линии x  = -2 ,  x = 0

Мы разделим нашу фигуру на две части , вычислим площадь каждой  части , а затем сложим их   чтобы найти площадь нашей фигуры

Мы получим участок ограниченный линиями   y =-x³/4 ,  y = x+4

Находим его площадь  :

$S_1 = \displaystyle \int\limits^0_{-2} \left ((x +4) - \left (-\frac{x^3}{4} \right)\right ) \, dx = \int\limits^0_{-2} \left (\frac{x^3}{4} +x +4\right )\, dx =\\\\\\ =\left ( \frac{x^4}{16} +\frac{x^2}{2}+4x \right ) \Bigg |^0_{-2} = 0 -\left (\frac{16}{16}+\frac{4}{2} - 8 \right) = -(3-8) = 5$

Находим площадь участка ограниченного линиями  y = x +4 ,   y =5x,  x =0

$S_2 = \displaystyle \int\limits^1_{0} (x+4-5x) \, dx = \int\limits^1_ {0} (-4x +4) \, dx =(-2x^2 +4x) \bigg |^1 _0 = -2 +4 + 0 = 2$


Тогда площадь искомой нами фигуры  равна :

$S= S_1 + S_2 = 5+2= 7$

#SPJ1