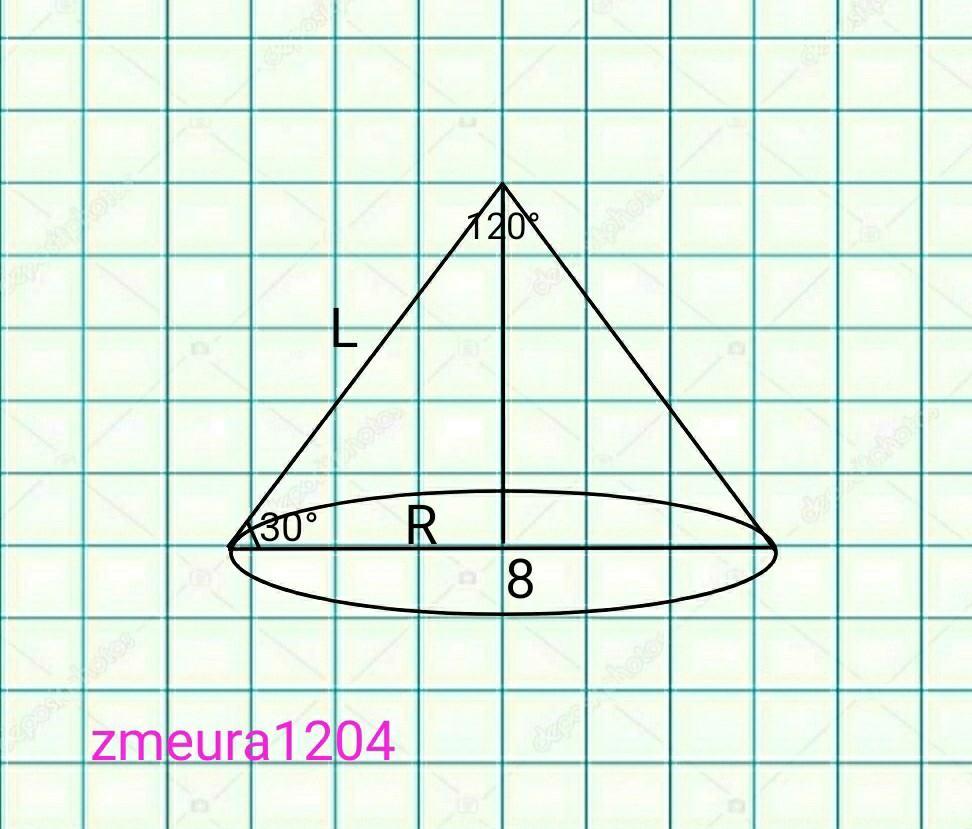
осьовий переріз конуса рівнобедрений трикутник з основою 8 см і кутом при вершині 120 градусів. Знайти площу повної поверхні та об'єм конуса.
Ответы
Відповідь:
Sпов=(48π32π√3)/3 см²
V=64π√3/9 см³
Розв'язання:
Кути при основі рівнобедреного трикутника рівні.
Сума кутів трикутника дорівнює 180°
(180°-120°)/2=60/2=30° кут при основі.
R=D/2=8/2=4см.
cos30°=R/L
cos30°=√3/2
√3/2=4/L
L=4*2/√3=8/√3=8√3/3.
Sбіч=πRL=π*4*8√3/3=32π√3/3 см²
Sосн=πR²=π*4²=16π см²
Sпов=Sбіч+Sосн=16π+32π√3/3=
=(48π+32π√3)/3 см²
За теоремою Піфагора
Н=√(L²-R²)=√((8/√3)²-4²)=√(64/3-16/1)=
=√(64/3-48/3)=√(16/3)=4√3/3 см
V=⅓*Sосн*Н=⅓*16π*4√3/3=64π√3/9 см³
Ответ:
Объяснение:
У конусі з вершиною М і осьовим перерізом АМВ АВ = 8 см ;
АМ = МВ ; ∠АМВ = 120° .
ΔАМВ - рівнобедрений , тому медіана МО є бісектрисою і
висотою . ОА = R = 1/2 AB = 1/2 * 8 = 4 ( см ) ; ∠AMO = 1/2 ∠AMB =
= 1/2 * 120° = 60° .
У прямок. ΔАОМ ctg60° = MO/AO ; MO = H =AO ctg60° = 4√3/3 ( см ) .
sin60° = AO/AM ; AM = L = AO/sin60° = 4/( √3/2 ) = 8√3/3 ( см ) .
S пов = πRL + πR² = πR( L + R ) = π * 4*( 8√3/3 +4) = 16π(2√3/3 + 1 ) ( см ) .
V кон = 1/3 πR²H = 1/3 π *4² * 4√3/3 = 16/9 π√3 ( см³ ) .