Предмет: Алгебра,
автор: Reideen
Найти неопределенные интегралы
Приложения:
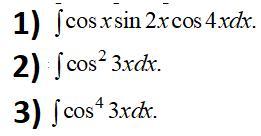
Ответы
Автор ответа:
2
Ответ:
1)
2)
3)
Примечание:
Формула понижения степени:
Преобразование произведения в сумму:
По таблице интегралов:
По свойствам интегралов:
Объяснение:
1)
2)
3)
------------------------------
а)
б)
в)
------------------------------
Похожие вопросы
Предмет: Русский язык,
автор: 123456789728
Предмет: Українська мова,
автор: glebsobolev228
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: zzzio
Предмет: Математика,
автор: bbilain54