Предмет: Алгебра,
автор: atajanowatajan1984
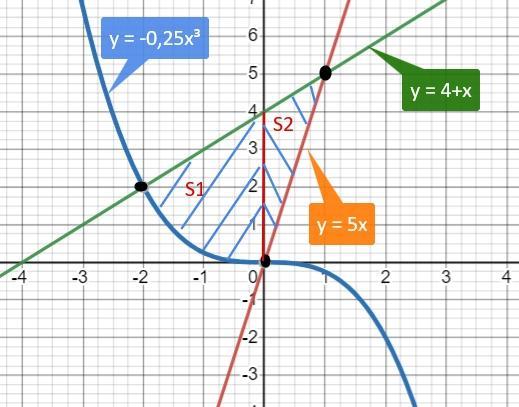
Вычислить площадь ограниченной заданными линиями y=-1/4x^3; y=4+x; y=5x.
Ответы
Автор ответа:
0
Ответ:
площадь фигуры равна 7
Объяснение:
Чертим графики
y = -0,25x³
y = 4 +x
y = 5x
По чертежу видим, что искомая площадь полученной фигуры состоит из двух площадей S1 и S2
Каждую площадь ищем отдельно по формуле Ньютона -Лейбница.
В обоих случаях график функции y = 4 +x лежит "выше" других графиков, поэтому именно ее принимаем за у₁(х).
Итого получим
S = S1 + S2 = 5 + 2 = 7
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: kbkbnfhvty
Предмет: Қазақ тiлi,
автор: пукиӘ
Предмет: Русский язык,
автор: антон647
Предмет: ОБЖ,
автор: vkookisreal163
Предмет: Математика,
автор: 709826