Question

УМОЛЯЮ ПОМОГИТЕ С АЛГЕБРОЙ

Answer 1

Ответ:

(см. объяснение)

Объяснение:

$|x|+|y|=a$ есть уравнение квадрата с длиной диагонали $2a$ и центром в точке $(0;\;0)$.

$|x|+|y|\le a$ есть неравенство, решением которого будут все точки внутри квадрата, а также на квадрате, поскольку знак неравенства нестрогий.

Неравенство $y > 5$ в комментариях не нуждается.

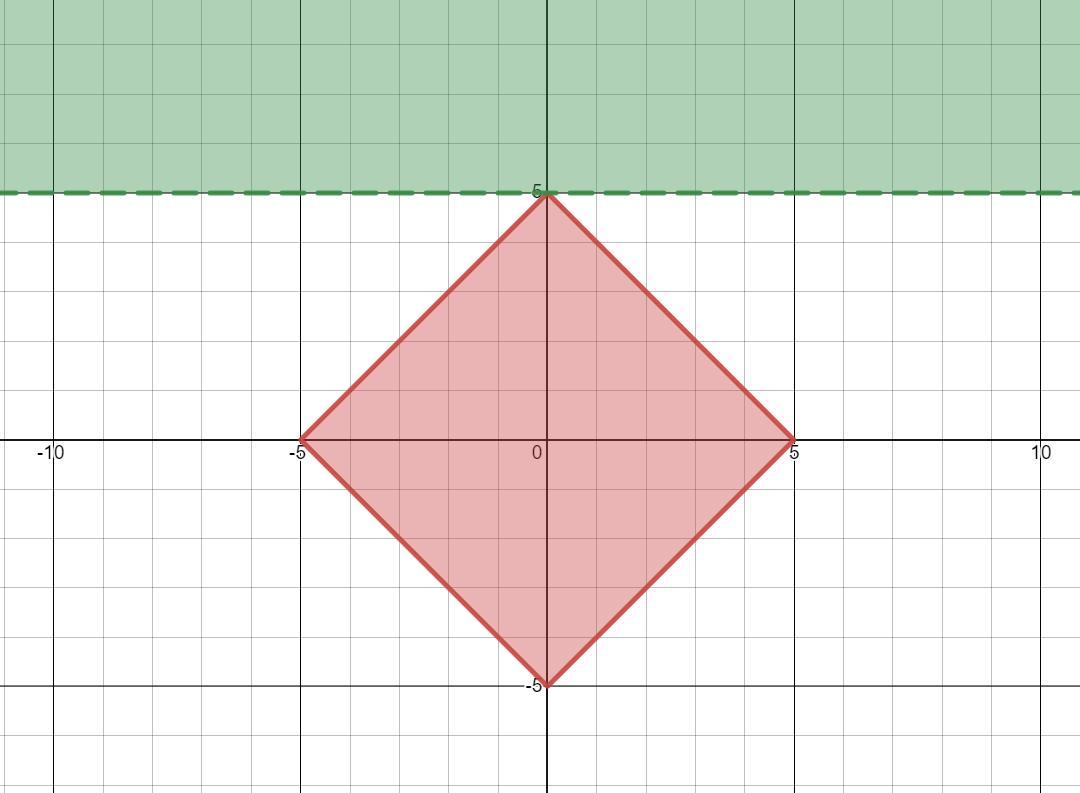
Построим решение системы в координатах $(x,\;y)$.

(см. прикрепленный файл)

Видим, что граничное положение, когда решений у системы еще нет есть случай, когда квадрат касается одной из своих вершин прямой $y=5$, то есть вершина квадрата тогда имеем координату $(0;\;5)$. При дальнейшем увеличении параметра квадрат будет расти, и решения будут всегда, причем их будет бесконечное множество уже при $a=5.000001$, скажем, например. Граничное положение достигается при $a=5$. Следовательно, $a > 5$ и ответ на задачу $6$.

Задание выполнено!