Предмет: Математика,
автор: PremiumArtur
Первообразные. Помогите!
Приложения:

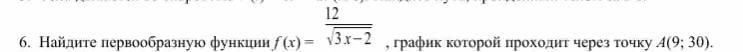
Ответы
Автор ответа:
1
Функция y=F(x) называется первообразной функции y=f(x) на промежутке Х, где для любого x ∈ X выполняется неравенство: F'(x)=f(x). То есть, чтобы найти первообразную F(x) нужно взять интеграл с f(x).
1) ∫
2) F(x) = ∫f(x)dx = ∫dx=
3) A(9;30)
Для начала, найдем общий вид первообразной, интегрируя заданную функцию
F(x) = ∫f(x)dx = ∫ =[Замена: t=x-2)= ∫
=4*2√t=4*2√(3x-2)=
Координаты точки А(9; 30), лежащей на графике первообразной, должны удовлетворять ее уравнению:
30=
30=
30=8*5+C
30=40+C
C=30-40=-10.
Подставив значение C в общее уравнение функции, найдем искомую первообразную:
=> F(x)=
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: ОлесяНабатчикова
Предмет: Другие предметы,
автор: карамелька1224
Предмет: Другие предметы,
автор: Family22