Предмет: Алгебра,
автор: elizavetakornienko18
помогите решить пожалуйста!! срочно. что сможете
Приложения:
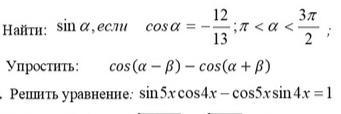
Ответы
Автор ответа:
0
Ответ:
1)
2)
3)
Объяснение:
1) По условию , надо найти
Так как , то угол
угол третьей четверти.
Воспользуемся основным тригонометрическим тождеством
Так как синус в третьей четверти отрицательный, то
2) Упростить :
Воспользуемся формулами
Получим
3) Решить уравнение
Воспользуемся формулой
и упростим левую часть уравнения . Получим
#SPJ1
Похожие вопросы
Предмет: Қазақ тiлi,
автор: neko7023
Предмет: Английский язык,
автор: poninya
Предмет: Русский язык,
автор: shvedovakk
Предмет: География,
автор: gare60