Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста с 2-ым номером , ДАЮ 50Баллов
Приложения:
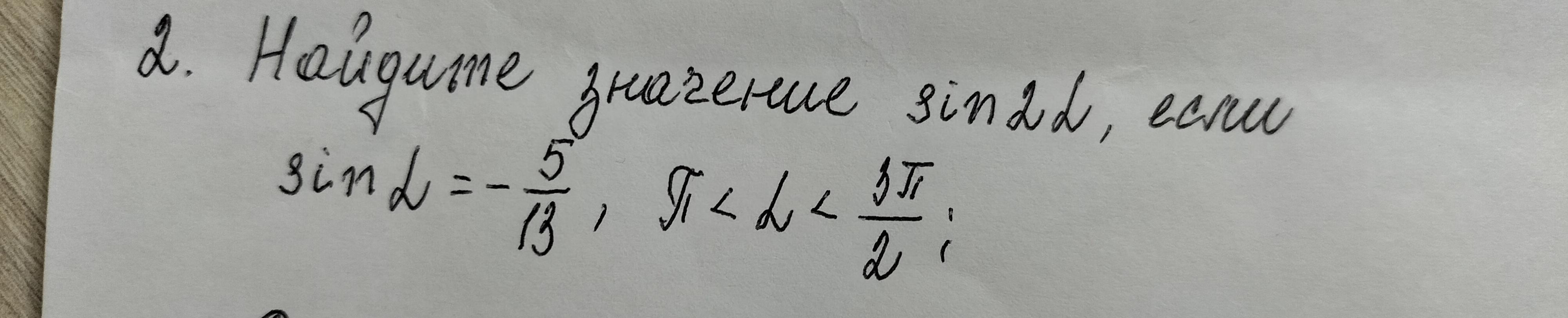
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Дано:
Найти:
sin2α - ?
Решение:
Необходимые формулы:
sin2α = 2sinα * cosα
Найдем cosα. Для этого выразим его из второго уравнения:
Так как , то cosα < 0. Тогда:
Теперь, подставив в первую формулу, найдем sin2α:
NNNLLL54:
минус упустили перед корнем: cosa= - sqrt{144/169}= - 12/13
Упс, да, исправил. Спасибо!
Похожие вопросы
Предмет: Окружающий мир,
автор: Xotunov
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: ника1776
Предмет: Другие предметы,
автор: registerskype
Предмет: Музыка,
автор: aleksandargotsvert