Предмет: Алгебра,
автор: Andzefrokin5864
Угол между высотой и биссектрисой, проведенными из вершины прямого угла прямоугольного треугольника, равен 80. Найдите острые углы треугольника.
genius20:
Этот угол не может быть равен 80°, он меняется в пределах от 0° до 45°, проверяйте условие.
Ответы
Автор ответа:
0
Ответ:
Решение с расчетом, если угол между высотой и биссектрисой равен 8°
37°, 53°
Объяснение:
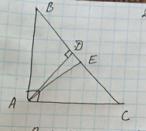
Дано: ΔАВС
∠ВАС=90°,
АД-высота , АЕ-биссектриса ∠А
∠ДАЕ=8°
Найти: ∠АВС-? ∠ВСА-?
Решение:
1. Рассмотрим Δ АДЕ:
∠АДЕ =90° (т.к. АД - высота)
∠ДАЕ =8° (по условию)
Следовательно, ∠ДЕА= 180°-∠АДЕ-∠ДАЕ
∠ДЕА=180°-90°-8°=82°
2. Рассмотрим Δ АЕС
∠ ЕАС= ∠ВАС = 90°:2=45° (т.к. АЕ- биссектриса)
∠АЕС=180°-∠ДЕА=180°-82°=98° (т.к.∠ ДЕА и ∠АЕС - смежные углы )
∠ВСА= 180°-∠ЕАС-∠АЕС=180°-45°-98°=37°
3. Рассмотрим Δ АВС
∠ВАС=90° (по условию)
∠ВСА=37°
∠АВС=180°-∠ВАС-∠ВСА=180°-90°-37°=53°
Ответ ∠АВС=53°, ∠ВСА=37°
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: igorpashinov
Предмет: Українська література,
автор: Анюта200556
Предмет: Немецкий язык,
автор: nun123
Предмет: Английский язык,
автор: kapitulskiy02
Предмет: Математика,
автор: timust7