Предмет: Алгебра,
автор: rodionbogoslavsky
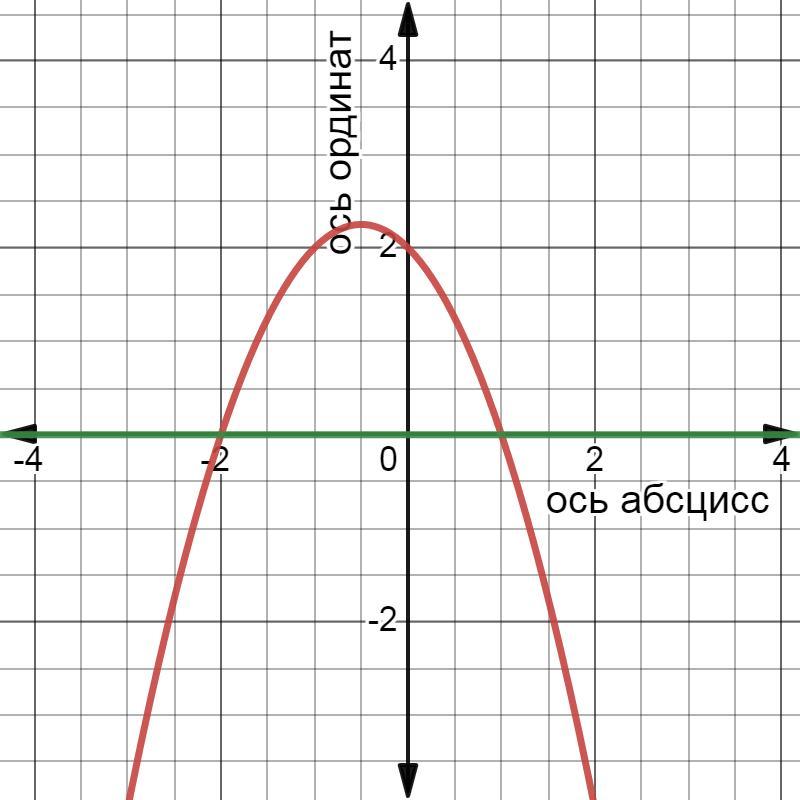
Найдите площадь фигуры ограниченной графиком функции f(x)=-x^2-x+2 и осью абсцисс, изобразив рисунок СРОЧНО, ПОЖАЛУЙСТА. Только точно
Ответы
Автор ответа:
1
Объяснение:
Ответ: S=4,5 кв. ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 89871367445
Предмет: Английский язык,
автор: pokrovskaya04
Предмет: Русский язык,
автор: Kein11
Предмет: Геометрия,
автор: chalovrodion38lololo
Предмет: Английский язык,
автор: karina4176