Предмет: Алгебра,
автор: 96vcrhwbbz
СРОЧНО, ДАЮ 20Б
1/х^2-2х -2/х =1/х^2-4
Приложения:
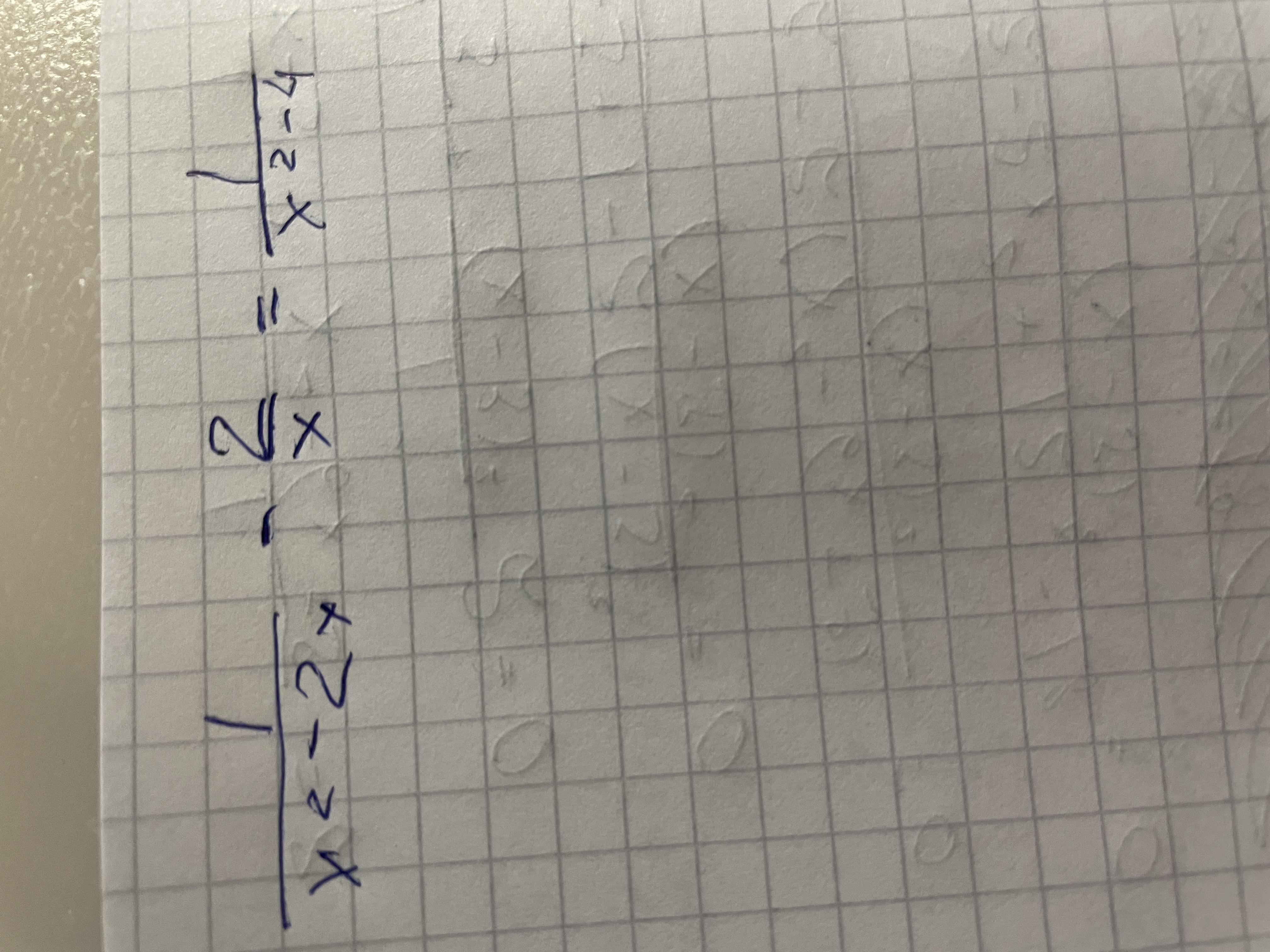
Ответы
Автор ответа:
1
Ответ:вот
Объяснение:
Приложения:

Автор ответа:
0
Решение.
, ОДЗ:
Приведём дроби к общему знаменателю .
Разложив по формуле разности квадратов левую часть равенства, приравниваем к 0 каждый множитель .
Похожие вопросы
Предмет: Русский язык,
автор: sabitov79
Предмет: Другие предметы,
автор: АринаПлатонова2005
Предмет: Английский язык,
автор: svetakotelniko
Предмет: Окружающий мир,
автор: diana201109
Предмет: Алгебра,
автор: GoGiDoGi