Предмет: Геометрия,
автор: vikmeniuk
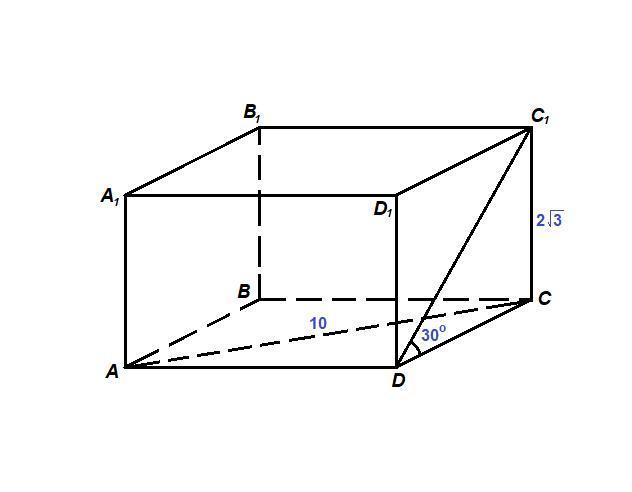
Бiчне ребро прямокутного паралелепіпеда дорівнює 2√3 см, а діагональ основи - 10 см. Знайдiть об'єм паралелепіпеда, якщо одна з діагоналей бічної грані нахилена до площини основи під кутом 30°.
Ответы
Автор ответа:
1
Ответ:
96√3 см³
Объяснение:
Все грани прямоугольного параллелепипеда - прямоугольники.
ΔCC₁D: ∠CC₁D = 90°,
DC = 6 см
ΔACD: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - DC²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
- Объем прямоугольного параллелепипеда равен произведению трех его измерений.
V = AD · DC · CC₁
V = 8 · 6 · 2√3 = 96√3 см³
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: loprapa
Предмет: Русский язык,
автор: maidov13
Предмет: Русский язык,
автор: холи1
Предмет: Другие предметы,
автор: KizDim
Предмет: Математика,
автор: dryg2686