Предмет: Геометрия,
автор: galaxyegor75
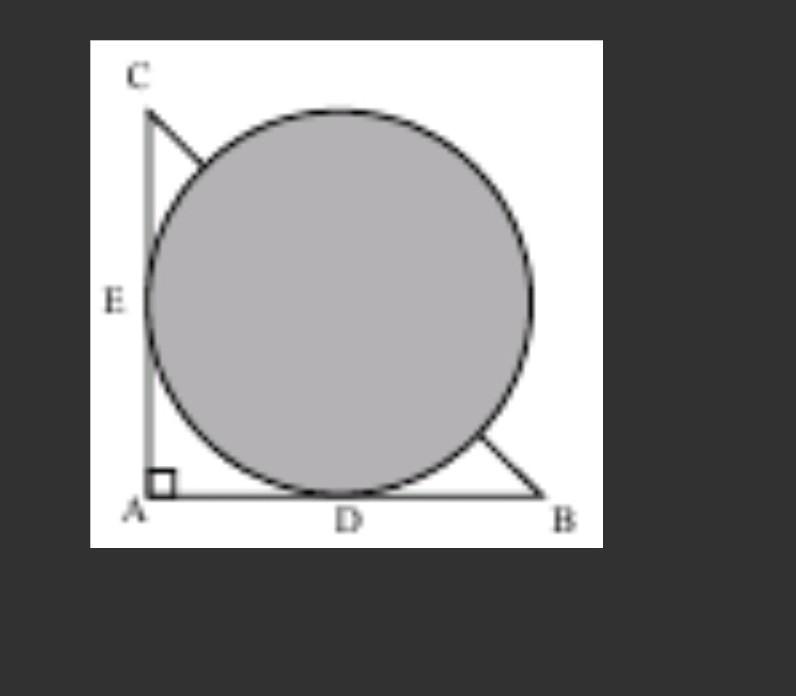
Диаметр нижеприведенного круга = 4. ABC - прямоугольный треугольник с AC = AB. AC и AB являются касательными к окружности в точках E и D соответственно. AE = EC. Какова площадь незатененной области?
Приложения:
Ответы
Автор ответа:
0
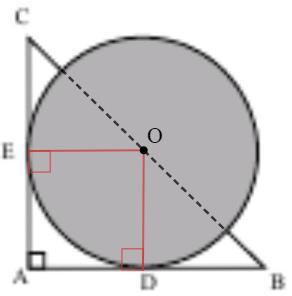
Проведем радиусы OD и OE в точки касания, они перпендикулярны касательным. AD=DB, AE=EC - получается, мы провели серединные перпендикуляры к катетами, а они в прямоугольном треугольнике пересекаются на гипотенузе (центр описанной окружности - середина гипотенузы). Таким образом точка O лежит на гипотенузе BC. Тогда часть BC внутри круга - диаметр, он делит круг пополам.
AEOD - квадрат (прямоугольник с равными смежными сторонами)
AD=OD=4/2=2; AB=2AD=4
Из площади треугольника вычитаем половину круга.
1/2 AB*AC - 1/2 п OD^2 = 8-2п
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: gabbasov252
Предмет: Английский язык,
автор: аида154
Предмет: Русский язык,
автор: polinka123999
Предмет: История,
автор: MrDragunooov
Предмет: Математика,
автор: savestyan