Предмет: Математика,
автор: ety1752
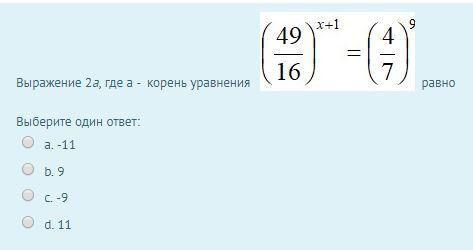
Выражение 2а, где а - корень уравнения (49/16)^x+1=(4/7)^9 равно
Приложения:
Ответы
Автор ответа:
0
Ответ:
Решение:
Формулы для решения:
Похожие вопросы
Предмет: Английский язык,
автор: Ґeek
Предмет: Русский язык,
автор: AinuraZhukenov1
Предмет: Русский язык,
автор: yana061102
Предмет: Физика,
автор: karinaturgunova05
Предмет: Французский язык,
автор: tparsiyants