Предмет: Алгебра,
автор: narknk06
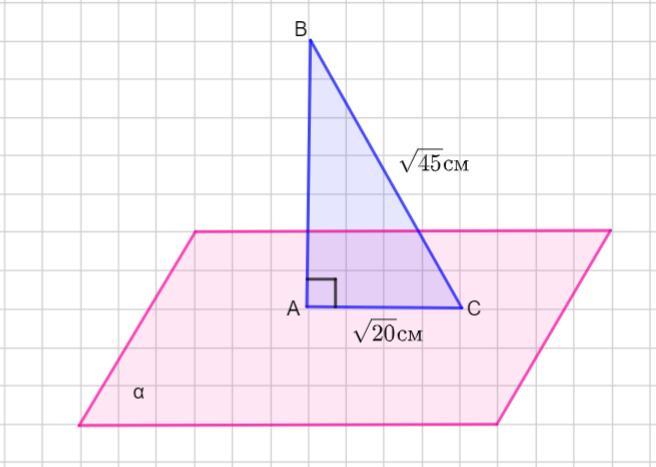
Із точки B до площини а проведено перпендикуляр та похилу довжиною √45 см проекція даної похилої на площину дорівнює√ 20 см Знайдіть відстань від точки B до площини а
Ответы
Автор ответа:
0
Ответ:
Расстояние от точки В до плоскости равно 5 см.
Объяснение:
Из точки В к плоскости проведен перпендикуляр ВА и наклонная ВС , АС - проекция наклонной на плоскость.
ВС= √45 см, АС= √20 см.
Надо найти расстояние от точки В до плоскости.
Расстоянием от точки до плоскости является длина перпендикуляра ВА.
Если ВА - перпендикуляр к плоскости, то ΔВАС - прямоугольный.
Воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда расстояние от точки В до плоскости равно 5 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Света6566755
Предмет: Русский язык,
автор: diana55665
Предмет: Русский язык,
автор: карина1335
Предмет: Окружающий мир,
автор: Asya6727