Question

найти точку максимума функции y=x^3+16x^2+64x+12

Answer 1

Ответ:

$x{_{max}} =-8 .$

Пошаговое объяснение:

Надо определить точку максимума функции

$y= x^{3} +16x^{2} +64x+12$

Областью определения данной функции является множество всех чисел, то есть D(y) = ( - ∞; +∞) .

Найдем производную данной функции

$y'= (x^{3} )'+(16x^{2} )'+(64x)'+12' =3x^{2} +16\cdot2x+64 =3x^{2} +32x+64$

Найдем критические точки, решив уравнение :

$y'=0.$

$3x^{2} +32x+64=0;\\\\\dfrac{D}{4} =16^{2} -3\cdot64=256-192= 64=8^{2} ;\\\\x{_1}= \dfrac{-16-8}{3} =\dfrac{-24}{3} =-8;\\\\x{_2}= \dfrac{-16+8}{3} =\dfrac{-8}{3} =-\dfrac{8}{3} .$

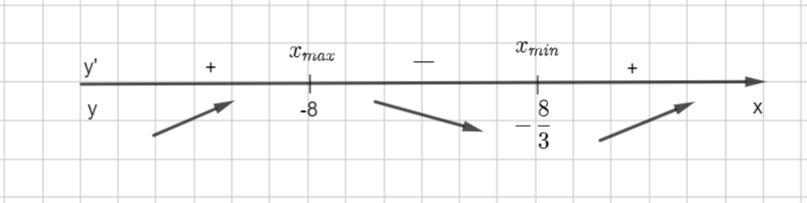
Полученные точки делят числовую прямую на три промежутка, определим знак производной на каждом промежутке ( показано во вложении)

Если при переходе через точку производная меняет свой знак с "+" на " -" , то данная точка является точкой максимума.

При переходе через х= -8 производная меняет свой знак с "+" на " -" Значит,

$x{_{max}} =-8$

#SPJ1