Предмет: Алгебра,
автор: timuribragimov6
Срочно помогите, пожалуйста
Приложения:
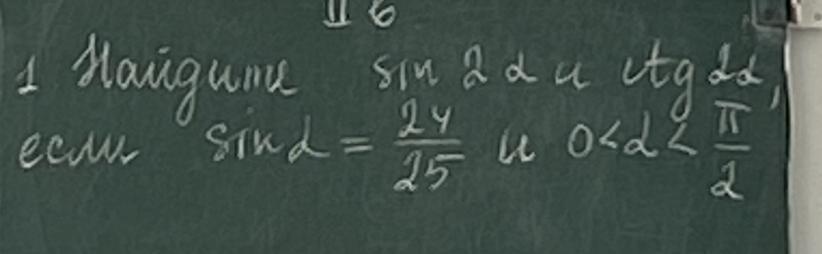
Ответы
Автор ответа:
3
Дано: sinα= ;
⇒
| четверти.
Найти: sin2α и ctg2α
Решение:
Используя тригонометрическое тождество : , выразим отсюда
.
Значение косинуса в 1-ой четверти- положительное , значит результат будет с положительным знаком :
Найдём , применив формулу двойного угла :
.
Чтобы найти - по формуле двойного угла:
, необходим
и
.
Найдём - по формуле:
.
, а
можем найти - если извлечём квадратный корень.
Значение котангенса в 1-ой четверти- положительное , значит результат будет с положительным знаком :
Теперь можно найти .
Ответ: sin2α=336/625 , ctg2α= - 527/336
Похожие вопросы
Предмет: Окружающий мир,
автор: motveibugaev
Предмет: Русский язык,
автор: monetka2005
Предмет: Русский язык,
автор: hagon
Предмет: Алгебра,
автор: GOLDUM
Предмет: Геометрия,
автор: pixuniv