Предмет: Математика,
автор: mariacrazygirl
какую плоскость рассмотреть?
Приложения:

Ответы
Автор ответа:
1
Ответ:
MX = 2
Пошаговое объяснение:
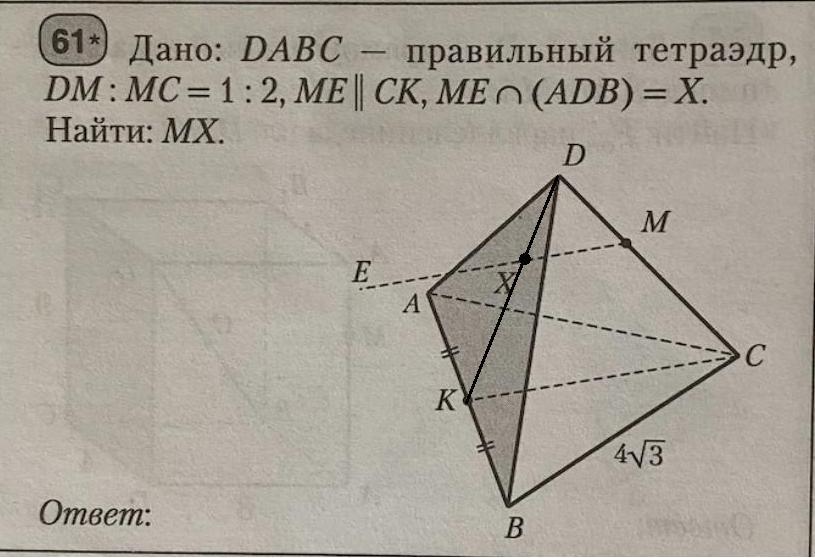
Параллельные прямые МЕ и СК задают плоскость α, в которой лежит ребро CD и точка К плоскости (ADB).
Тогда α ∩ (ADB) = DK.
Прямая МЕ пересекает DK в точке Х.
СК - высота равностороннего треугольника, значит
- Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
МХ║СК, значит
ΔMDX ~ ΔCDK.
DM : MC = 1 : 2, значит DM : DC = 1 : 3
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: lolipop71
Предмет: Русский язык,
автор: Max0005
Предмет: Қазақ тiлi,
автор: 200091
Предмет: Русский язык,
автор: ivanshematuhin1