Question

ДОПОМОЖІТЬ....... геометрія

Answer 1

Ответ:

Третья сторона треугольника равна 2 см или 2√5 см.

Задача имеет два решения.

Объяснение:

По следствию из теоремы синусов:

• отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности:

$\dfrac{a}{\sin\angle A}=2R$

$\sin\angle A =\dfrac{a}{2R}$

По условию $\dfrac{a}{R}=\dfrac{\sqrt{2}}{1}$, тогда

$\sin\angle A=\dfrac{\sqrt{2}}{2}$

Так как sin(180° - ∠A) = sin∠A, то нельзя однозначно определить угол.

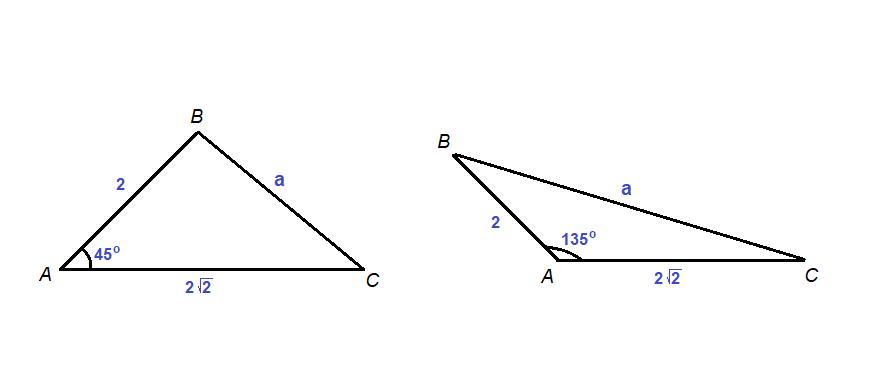
∠А = 45° или ∠А = 135°.

1. ∠А = 45°

$\cos 45^\circ=\dfrac{\sqrt{2}}{2}$

По теореме косинусов:

a² = AB² + AC² - 2 · AB · AC · cos∠A

$a^2=2^2+(2\sqrt{2})^2-2\cdot 2\cdot 2\sqrt{2}\cdot \dfrac{\sqrt{2}}{2}$

a² = 4 + 8 - 8 = 4

a = 2 см

2. ∠А = 135°

$\cos 135^\circ=-\dfrac{\sqrt{2}}{2}$

По теореме косинусов:

a² = AB² + AC² - 2 · AB · AC · cos∠A

$a^2=2^2+(2\sqrt{2})^2+2\cdot 2\cdot 2\sqrt{2}\cdot \dfrac{\sqrt{2}}{2}$

a² = 4 + 8 + 8 = 20

a = √20 = 2√5 см